题目内容
15.已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,则称集合M具有∟性,给出下列四个集合:①M={(x,y)|y=x3-2x2+3}; ②M={(x,y)|y=log2(2-x)};
③M={(x,y)|y=2-2x}; ④M={(x,y)|y=1-sinx};
其中具有∟性的集合的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 条件等价于:对于M中任意点P(x1,y1),在M中存在另一个点P′(x2,y2),使OP⊥OP′.作出函数图象,验证即可.
解答 解:由题意知:对于M中任意点P(x1,y1),在M中存在另一个点P′(x2,y2),使$\overrightarrow{OP}•\overrightarrow{OP′}=0$,即OP⊥OP′,即过原点任作一条直线与函数图象相交,都能过原点作另一条直线与此直线垂直,经验证①②③④皆满足.
故选:D.
点评 本题考查集合的表示方法、函数图象及其应用,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
6.某高中要从该校三个年级中各选取1名学生参加校外的一项知识问答活动,若高一、高二、高三年级分别有5,6,8个学生备选,则不同选法有( )
| A. | 19种 | B. | 38种 | C. | 120种 | D. | 240种 |
3.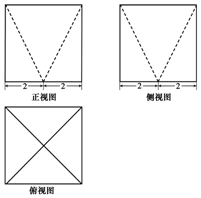 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
10. 一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
 一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )
一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )| A. | 24 | B. | 48 | C. | 72 | D. | 96 |
4.在复平面内,复数z=$\frac{1-i}{i}$(i是虚数单位)对应的点的坐标是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |
5.设集合$A=\{x|\frac{1}{4}≤{2^x}≤16\}$,$B=\{x|\frac{2x-3}{x-3}>1\}$,则A∩B=( )
| A. | {x|-2≤x<0或3<x≤4} | B. | {x|-2≤x≤0或3≤x≤4} | C. | {x|-2<x≤4} | D. | {x|0<x<3} |
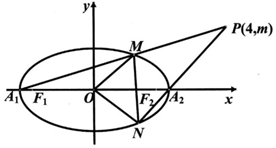 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.