题目内容
12.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,收到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如表所示:| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
(2)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
分析 (1)由题意可知:$m+n+\frac{1}{6}+\frac{1}{3}=1$,再由m=2n,能求出这60名抗战老兵中参加纪念活动的环节数为0,1,2,3的抗战老兵的人数分别为10,20,10,20,由此利用分层抽样法能求出参加纪念活动的环节数为1的抗战老兵中应抽取的人数.
(2)抽取的这6名抗战老兵中1名参加了0个环节,记为A,2名参加了1个环节,记为B,C,1名参加了2个环节,分别记为D,2名参加了3个环节,分别记为E,F,从这6名抗战老兵中随机抽取2人,利用列举法能求出这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
解答 解:(1)由题意可知:$m+n+\frac{1}{6}+\frac{1}{3}=1$,
又m=2n,解得$m=\frac{1}{3}$,$n=\frac{1}{6}$
故这60名抗战老兵中参加纪念活动的环节数为0,1,2,3的抗战老兵的人数分别为10,20,10,20,
其中参加纪念活动的环节数为1的抗战老兵中应抽取的人数为$20×\frac{6}{60}=2$.
(2)由(1)可知抽取的这6名抗战老兵中1名参加了0个环节,记为A,
2名参加了1个环节,记为B,C,1名参加了2个环节,分别记为D,
2名参加了3个环节,分别记为E,F,
从这6名抗战老兵中随机抽取2人,有:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),
(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),
共15个基本事件,
记“这2名抗战老兵中至少有1人参加纪念活动的环节数为3”位事件M,
则事件M包含的基本事件为:
(A,E),(A,F),(B,E),(B,F),(C,E),(C,F),
(D,E),(D,F),(E,F),共9个基本事件.
所以这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率$P(M)=\frac{9}{15}=\frac{3}{5}$.
点评 本题分层抽样的应用,考查概率的求法,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、数形结合思想,是基础题.

 阶梯计算系列答案
阶梯计算系列答案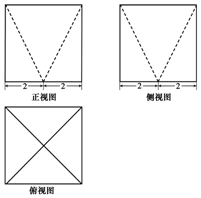 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
| A. | 66 | B. | 99 | C. | 198 | D. | 297 |
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
| A. | (0,$\frac{3}{4}$] | B. | (0,1] | C. | [$\frac{3}{4}$,1] | D. | [$\frac{3}{2}$,1] |
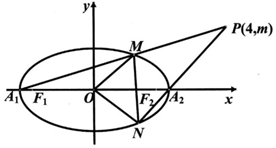 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右项点分别为A1,A2,左右焦点分别为F1,F2,离心率为$\frac{\sqrt{3}}{2}$,|F1F2|=2$\sqrt{3}$,O为坐标原点.