题目内容
13.由y=(x-2)2与y=4x-8所围图形的面积为( )| A. | 6 | B. | $\frac{54}{3}$ | C. | $\frac{32}{3}$ | D. | 9 |
分析 利用定积分知识求解该区域面积是解决本题的关键,要确定出y=(x-2)2与y=4x-8的交点,确定出积分区间和被积函数,利用导数和积分的关系完成本题的求解.
解答 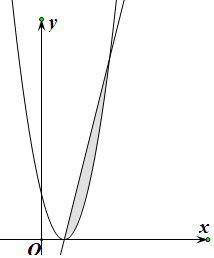 解:联立方程组可得$\left\{\begin{array}{l}{y=(x-2)^{2}}\\{y=4x-8}\end{array}\right.$,解得x=2或x=6,
解:联立方程组可得$\left\{\begin{array}{l}{y=(x-2)^{2}}\\{y=4x-8}\end{array}\right.$,解得x=2或x=6,
故由y=(x-2)2与y=4x-8所围图形的面积为
S=${∫}_{2}^{6}$[4x-8-(x-2)2]dx=${∫}_{2}^{6}$(8x-12-x2)dx=(4x2-12x-$\frac{1}{3}$x3)|${\;}_{2}^{6}$=(144-72-72)-(16-24-$\frac{8}{3}$)=$\frac{32}{3}$,
故选:C
点评 本题考查曲边图形面积的计算问题,考查学生分析问题解决问题的能力和意识,考查学生的转化与化归能力和运算能力,考查学生对定积分与导数的联系的认识,求定积分关键要找准被积函数的原函数,属于定积分的简单应用问题.

练习册系列答案
相关题目
3.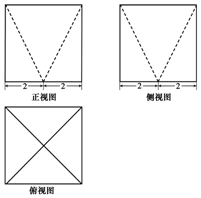 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
4.在复平面内,复数z=$\frac{1-i}{i}$(i是虚数单位)对应的点的坐标是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |
1.若a,b,c分别是角A,B,C的对边,若a=b=$\frac{\sqrt{3}}{3}$c,则角A=( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
18.若0<m<n<2,e为自然对数的底数,则下列各式中一定成立的是( )
| A. | men<nem | B. | men>nem | C. | mlnn>nlnm | D. | mlnn<nlnm |
5.设集合$A=\{x|\frac{1}{4}≤{2^x}≤16\}$,$B=\{x|\frac{2x-3}{x-3}>1\}$,则A∩B=( )
| A. | {x|-2≤x<0或3<x≤4} | B. | {x|-2≤x≤0或3≤x≤4} | C. | {x|-2<x≤4} | D. | {x|0<x<3} |
2.已知函数f(x)=2sinωx+1(ω>0)在区间[-$\frac{π}{2}$,$\frac{2π}{3}$]上是增函数,则ω的取值范围是( )
| A. | (0,$\frac{3}{4}$] | B. | (0,1] | C. | [$\frac{3}{4}$,1] | D. | [$\frac{3}{2}$,1] |
3.设集合A={x|x2+x-6<0},B={x|1≤x≤3},则A∩B=( )
| A. | [1,2] | B. | [1,2) | C. | [2,3] | D. | (2,3] |