题目内容
8．（1）从1，2，3，4四个数字中任取两个数字组成两位数，共有多少个不同的两位数？（2）由1，2，3，4四个数字共能组成多少个没有重复数字的四位数？
分析 （1）根据题意，由排列数公式计算即可得答案；
（2）根据题意，将4个数字全排列即可得四位数的个数，由排列数公式计算可得答案．
解答 解：（1）根据题意，要求从1，2，3，4四个数字中任取两个数字组成两位数，
则一共有A42=12种不同的取法，
即共有12个不同的两位数；
（2）根据题意，要求用1，2，3，4四个数字组成没有重复数字的四位数，
将4个数字全排列即可，
有A44=24种不同的排法，即有24个没有重复数字的四位数．
点评 本题考查排列数公式的应用，注意区分排列数与组合数公式的不同．
练习册系列答案
相关题目
18．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线的方程是y=$\frac{\sqrt{3}}{2}$x，且双曲线的一个焦点在抛物线y2=4$\sqrt{7}$x的准线上，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{21}-\frac{{y}^{2}}{28}$=1 | B． | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{3}$=1 | C． | $\frac{{x}^{2}}{28}-\frac{{y}^{2}}{21}$=1 | D． | $\frac{{x}^{2}}{3}-\frac{{y}^{2}}{4}$=1 |
16．复数$\frac{（-1+\sqrt{3}i）^{5}}{1+\sqrt{3}i}$的值是（ ）
| A． | -16 | B． | 16 | C． | -$\frac{1}{4}$ | D． | $\frac{1}{4}$-$\frac{\sqrt{3}}{4}$i |
3．
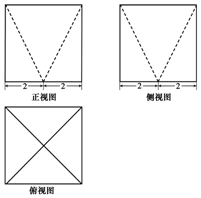某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的表面积是（ ）
某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的表面积是（ ）| A． | $96+16\sqrt{5}$ | B． | $80+16\sqrt{5}$ | C． | $80+32\sqrt{5}$ | D． | $96+32\sqrt{5}$ |