题目内容
18．已知x∈（0，+∞），观察下列各式：$x+\frac{1}{x}＞2，x+\frac{4}{x^2}=\frac{x}{2}+\frac{x}{2}+\frac{4}{x^2}≥3，x+\frac{27}{x^3}=\frac{x}{3}+\frac{x}{3}+\frac{27}{x^3}≥4，…$类比得$x+\frac{a}{x^n}≥n+1（{n∈{N^*}}）$，则a=nn．分析 观察前几个式子的分子分母可发现规律得出结论．
解答 解：当n=1时，a=1，
当n=2时，a=2=22，
当n=3时，a=27=33，
…
∴当分母指数取n时，a=nn．
故答案为nn．
点评 本题考查了归纳推理，寻找规律是关键．
练习册系列答案
相关题目
6．某高中要从该校三个年级中各选取1名学生参加校外的一项知识问答活动，若高一、高二、高三年级分别有5，6，8个学生备选，则不同选法有（ ）
| A． | 19种 | B． | 38种 | C． | 120种 | D． | 240种 |
13．已知向量$\overrightarrow{a}$=（sinx，cosx），$\overrightarrow{b}$=（sinx+cosx，sinx-cosx）（x∈R），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x的取值集合为（ ）
| A． | {x|x=$\frac{kπ}{2}$+$\frac{π}{8}$，k∈Z} | B． | {x|x=kπ+$\frac{π}{8}$，k∈Z} | C． | {x|x=$\frac{kπ}{2}$+$\frac{π}{4}$，k∈Z} | D． | {x|x=kπ+$\frac{π}{4}$，k∈Z} |
3．
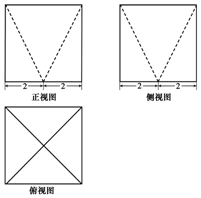某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的表面积是（ ）
某几何体的三视图如图所示，图中的四边形都是边长为4的正方形，两条虚线互相垂直，则该几何体的表面积是（ ）| A． | $96+16\sqrt{5}$ | B． | $80+16\sqrt{5}$ | C． | $80+32\sqrt{5}$ | D． | $96+32\sqrt{5}$ |
10．
一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示，则该几何体的体积为（ ）
一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示，则该几何体的体积为（ ）| A． | 24 | B． | 48 | C． | 72 | D． | 96 |
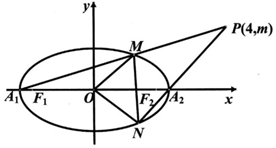如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右项点分别为A1，A2，左右焦点分别为F1，F2，离心率为$\frac{\sqrt{3}}{2}$，|F1F2|=2$\sqrt{3}$，O为坐标原点．