题目内容
14.(x-$\frac{1}{2x}$)8的展开式中常数为( )| A. | $\frac{1}{2}$ | B. | $\frac{35}{8}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
分析 利用二项式展开式的通项公式,即可求出展开式的常数项.
解答 解:(x-$\frac{1}{2x}$)8展开式中,通项公式为:
Tr+1=${C}_{8}^{r}$•x8-r•(-$\frac{1}{2}$)r•x-r=(-$\frac{1}{2}$)r•${C}_{8}^{r}$•x8-2r,
令8-2r=0,解得r=4;
所以展开式中常数项为第5项,为${(-\frac{1}{2})}^{4}$•${C}_{8}^{4}$=$\frac{35}{8}$.
故选:B.
点评 本题考查了二项式展开式的通项公式应用问题,是基础题.

练习册系列答案
相关题目
6.某高中要从该校三个年级中各选取1名学生参加校外的一项知识问答活动,若高一、高二、高三年级分别有5,6,8个学生备选,则不同选法有( )
| A. | 19种 | B. | 38种 | C. | 120种 | D. | 240种 |
3.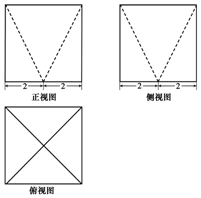 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的表面积是( )| A. | $96+16\sqrt{5}$ | B. | $80+16\sqrt{5}$ | C. | $80+32\sqrt{5}$ | D. | $96+32\sqrt{5}$ |
4.在复平面内,复数z=$\frac{1-i}{i}$(i是虚数单位)对应的点的坐标是( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-1,1) |