题目内容

1．过点P（x0，y0）与直线Ax+By+C=0垂直的直线方程是（　　）
A．A（x-x0）+B（y-y0）=0B．B（x-x0）+A（y-y0）=0C．A（x-x0）-B（y-y0）=0D．B（x-x0）-A（y-y0）=0

分析 根据题意，设要求直线的方程为Bx-Ay+m=0，将点P的坐标代入其方程可得m的值，再将m的值代入直线方程，变形即可得答案．

解答 解：根据题意，要求直线与直线Ax+By+C=0垂直，
可以设其方程为Bx-Ay+m=0，
又由其过点P（x0，y0），则有Bx0-Ay0+m=0，即m=-（Bx0-Ay0），
则要求直线的方程为：Bx-Ay-（Bx0-Ay0）-0，
即B（x-x0）-A（y-y0）=0，
故选：D．

点评 本题考查直线的点斜式方程，注意两直线垂直时其斜率之间的关系．

练习册系列答案
相关题目
15．已知直线过点P（2，1）．
（1）若直线与3x-2y+4=0平行，求直线的方程．
（2）若直线与3x-2y+4=0垂直，求直线的方程．
（3）若直线在两坐标轴上的截距相等，求直线的方程．
15．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x＜0}\\{-{x}^{2}+2x，x≥0}\end{array}\right.$，则f（2）=0．若f（f（x））≥9，则实数x的取值范围是[3，+∞）．
10．在平面直角坐标系中，曲线C的参数方程为：$\left\{\begin{array}{l}x=\sqrt{5}cosθ\\ y=3+\sqrt{5}sinθ\end{array}\right.$（其中θ为参数）．
（Ⅰ） 以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，求曲线C的极坐标方程；
（ II）直线l的参数方程为：$\left\{\begin{array}{l}x=tcosα\\ y=tsinα\end{array}\right.$（其中t为参数），直线l与曲线C分别交于A，B两点，且$|AB|=2\sqrt{3}$，求直线l的斜率．

已知函数,如果不等式的解集是则不等式的解集是___________
5．在△ABC中，角A，B，C的对边分别为a，b，c，已知2ccosB+b=2a，b=6，a=4．
（1）求角C的大小；
（2）若点D在AB边上，AD=CD，求CD的长．
11．点P是曲线C1：（x-2）2+y2=4上的动点，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，以极点O为中心，将点P逆时针旋转90°得到点Q，设点Q的轨迹方程为曲线C2．
（1）求曲线C1，C2的极坐标方程；
（2）射线θ=$\frac{π}{3}（{ρ＞0}）$与曲线C1，C2分别交于A，B两点，定点M（2，0），求△MAB的面积．
8．已知abcd≠0，则“a，b，c，d成等比数列”是“ad=bc”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

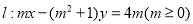已知直线和圆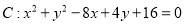．有以下几个结论：

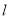①直线的倾斜角不是钝角；

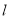②直线必过第一、三、四象限；

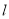③直线能将圆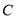分割成弧长的比值为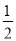的两段圆弧；

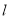④直线与圆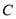相交的最大弦长为．

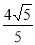其中正确的是________________．（写出所有正确说法的番号）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网