题目内容
15.过点P(1,2)作直线m,使直线l与点M(2,3)和点N(4,9)距离相等,则直线m的方程为3x-y-1=0或2x-y=0..分析 求出直线l与MN平行时和直线l经过线段MN的中点时对应的直线方程,再化为一般方程即可.
解答 解:①当直线l与MN平行时,
kMN=$\frac{9-3}{4-2}$=3,
∴直线l的方程为:y-2=3(x-1),
化为一般方程为:3x-y-1=0;
②当直线l经过线段MN的中点C(3,6)时,
kPC=$\frac{6-2}{3-1}$=2,
∴直线l的方程为:y-2=2(x-1),
化为一般方程是:2x-y=0;
综上,所求的直线方程为3x-y-1=0或2x-y=0.
故答案为:3x-y-1=0或2x-y=0.
点评 本题考查了相互平行的直线斜率之间的关系、中点坐标公式、直线方程以及分类讨论方法的应用问题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )
如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )
 如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )
如图所示,两个非共线向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为θ,N为OB中点,M为OA上靠近A的三等分点,点C在直线MN上,且$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x、y∈R),则x2+y2的最小值为( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{5}$ | C. | $\frac{4}{9}$ | D. | $\frac{2}{3}$ |
1.在△ABC中,内角A,B,C所对的边长分别为a,b,c.asinBcosC+csinBcosA=$\frac{1}{2}$b且a>b,则∠B=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{6}$ |
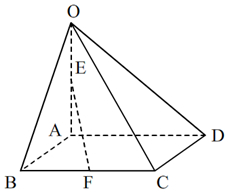 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,OA⊥面ABCD,OA=4,E点为OA的中点,F为BC中点,