题目内容
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
(Ⅰ)求异面直线EF和PB所成角的大小;
(Ⅱ)求证:平面PCE⊥平面PBC;
(Ⅲ)求二面角E-PC-D的大小.

解:以直线AB为x轴,直线AD为z轴建立间直角坐标系,如图,则
A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
 (Ⅰ)∵E为AD中点,∴E(0,1,0).又F为PC中点,
(Ⅰ)∵E为AD中点,∴E(0,1,0).又F为PC中点,
∴F(1,1,1).∴ 又
又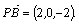
∴cos<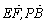 >=90°,∴异面直线EF和PB所成角
>=90°,∴异面直线EF和PB所成角
的大小为90°. ……………4分
(Ⅱ)由(Ⅰ)知EF⊥PB,又∵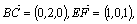
∴ ∴EF⊥BC.∴EF⊥平面PBC,又EF
∴EF⊥BC.∴EF⊥平面PBC,又EF 平面PCE,∴平面PCE⊥平面PBC. …8分 (Ⅲ)过点D作DH⊥PC于H. 在Rt△PDC中,PD=2
平面PCE,∴平面PCE⊥平面PBC. …8分 (Ⅲ)过点D作DH⊥PC于H. 在Rt△PDC中,PD=2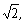 DC=2,PC=2
DC=2,PC=2
则CH= :HC=2:1, 又P(0,0,2),C(2,2,0). ∵H(
:HC=2:1, 又P(0,0,2),C(2,2,0). ∵H( ).
).
∴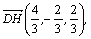 又
又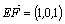 ,∴cos<
,∴cos< >=
>=
∴< >=30°. ………12分∴二面角E-PC-D的大小为30°. ………13分
>=30°. ………12分∴二面角E-PC-D的大小为30°. ………13分

练习册系列答案
相关题目
 和
和 ,则两圆的位置关系为
,则两圆的位置关系为 设实数
设实数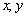 满足约束条件
满足约束条件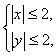 则
则 的取值范围是( )
的取值范围是( )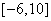 B.
B. C.
C.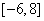 D.
D.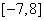
 若直线
若直线 与函数
与函数 的图象有两个不同的交点,则实数
的图象有两个不同的交点,则实数 的取值范围是( )
的取值范围是( ) B.
B.  C.
C.  D.
D. 
 的展开式中恰好第5项的二项式系数最大,则展开式中含
的展开式中恰好第5项的二项式系数最大,则展开式中含 项的系数是___ .
项的系数是___ . .
. ,并说明等号成立的条件;
,并说明等号成立的条件; 的不等式
的不等式 恒成立,求实数
恒成立,求实数 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( )
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ) B.
B. C.
C. D.
D.