题目内容
定义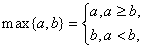 设实数
设实数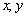 满足约束条件
满足约束条件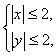 则
则 的取值范围是( )
的取值范围是( )
A.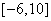 B.
B. C.
C.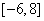 D.
D.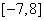
B

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
题目内容
定义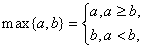 设实数
设实数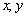 满足约束条件
满足约束条件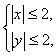 则
则 的取值范围是( )
的取值范围是( )
A.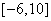 B.
B. C.
C.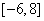 D.
D.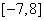
B

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案