题目内容
函数y=2-x+x2-4的零点个数为 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:要判断函数f(x)=2-x+x2-4的零点的个数,即函数y=2-x与函数y=-x2+3的图象的交点个数,数形结合,即可得到答案.
解答:
 解:函数y=2-x+x2-4的零点个数,
解:函数y=2-x+x2-4的零点个数,
即函数y=2-x和函数y=4-x2 的图象的交点个数,
数形结合可得,函数y=2-x的图象(蓝色部分)
和函数y=4-x2 的图象(红色部分)的交点个数为2,
故答案为:2.
 解:函数y=2-x+x2-4的零点个数,
解:函数y=2-x+x2-4的零点个数,即函数y=2-x和函数y=4-x2 的图象的交点个数,
数形结合可得,函数y=2-x的图象(蓝色部分)
和函数y=4-x2 的图象(红色部分)的交点个数为2,
故答案为:2.
点评:本题主要考查方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
若函数f(x)的图象上存在不同两点A,B,设线段AB的中点为M(x0,y0),使得f(x)在点(x0,f(x0))处的切线l与直线AB平行或重合,则称切线l为函数f(x)的“平衡切线”.则函数f(x)=2aln(x+1)+x2-2x的“平衡切线”的条数为( )
| A、2条或无数条 |
| B、1条或无数条 |
| C、0条或无数条 |
| D、2条或0条 |
在数列{an}中,a1=2,an+1=an+ln(1+
),则an=( )
| 1 |
| n |
| A、2+ln n |
| B、2+(n-1)ln n |
| C、2+n ln n |
| D、1+n+ln n |
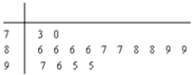 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):

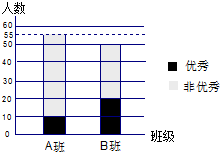 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.