题目内容
已知数列{an}满足a1=2,an-+1=2(1+
)2an
(1)求数列{an}的通项公式;
(2)设bn=(An2+Bn+C)•2n,试推断是否存在常数A、B、C,使对于一切n∈N*都有an=bn+1-bn成立?若存在,求出A,B,C的值;若不存在,说明理由.
(3)求:
an.
| 1 |
| n |
(1)求数列{an}的通项公式;
(2)设bn=(An2+Bn+C)•2n,试推断是否存在常数A、B、C,使对于一切n∈N*都有an=bn+1-bn成立?若存在,求出A,B,C的值;若不存在,说明理由.
(3)求:
| ||
| n=1 |
考点:数列递推式
专题:等差数列与等比数列
分析:(1)把已知的数列递推式变形,得到数列{
}是公比为2的等比数列,求其通项公式后得答案;
(2)求出bn+1-bn,由对于一切n∈N*都有an=bn+1-bn成立比较系数求得A,B,C的值;
(3)直接利用an=bn+1-bn裂项相消求得
an.
| an |
| n2 |
(2)求出bn+1-bn,由对于一切n∈N*都有an=bn+1-bn成立比较系数求得A,B,C的值;
(3)直接利用an=bn+1-bn裂项相消求得
| ||
| n=1 |
解答:
解:(1)由an-+1=2(1+
)2an=
an,得
=2
,
∴数列{
}是公比为2的等比数列.
首项a1=2,
∴
=2n,即an=2n•n2;
(2)∵bn=(An2+Bn+C)•2n,
∴bn+1-bn=[An2+(4A+B)n+2A+2B+C]•2n,
由对于一切n∈N*都有an=bn+1-bn成立,得
,解得A=1,B=-4,C=6;
(3)
an=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)
=bn+1-b1=(n2-2n+3)•2n+1-6.
| 1 |
| n |
| 2(n+1)2 |
| n2 |
| an+1 |
| (n+1)2 |
| an |
| n2 |
∴数列{
| an |
| n2 |
首项a1=2,
∴
| an |
| n2 |
(2)∵bn=(An2+Bn+C)•2n,
∴bn+1-bn=[An2+(4A+B)n+2A+2B+C]•2n,
由对于一切n∈N*都有an=bn+1-bn成立,得
|
(3)
| ||
| n=1 |
=bn+1-b1=(n2-2n+3)•2n+1-6.
点评:本题考查了数列递推式,考查了等比关系的确定,训练了比较系数法求函数解析式,考查了裂项相消法求数列的和,是中档题.

练习册系列答案
相关题目
已知奇函数f(x)在(-∞,0)上是单调减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为( )
| A、{x|-3<x<-1} |
| B、{x|-1<x<1或1<x<3} |
| C、{x|-3<x<0或1<x<3} |
| D、{x|-3<x<1或x>2} |

 将各项均为正整数的数列{an}排成如图所示的三角形数阵(第n行有n个数;在同一行中,各项的下标从左到右依次增大).bn表示该数阵中第n行第1个数.已知数列{bn}为公比为q等比数列,a1=1,a3=a2+1,且从第3行开始,从左到右,各行均构成公差为d的等差数列.
将各项均为正整数的数列{an}排成如图所示的三角形数阵(第n行有n个数;在同一行中,各项的下标从左到右依次增大).bn表示该数阵中第n行第1个数.已知数列{bn}为公比为q等比数列,a1=1,a3=a2+1,且从第3行开始,从左到右,各行均构成公差为d的等差数列.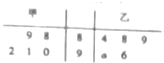 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0-9的某个整数