题目内容
已知函数f(x)=
(1)若a=1,求方程|f(x)|=5的解.
(2)若f(x)在(-∞,+∞)是单调递增的,求实数a的范围?
|
(1)若a=1,求方程|f(x)|=5的解.
(2)若f(x)在(-∞,+∞)是单调递增的,求实数a的范围?
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)当x≤1时,f(x)=-x2+2x-2,图象是抛物线的一部分;当1<x≤2时,f(x)=-
,图象是反比例函数图象的一部分;若a=1,x>2时,函数f(x)=x+1-1=x,图象是y=x的图象的一部分,可画出分段函数的图象,结合图象解方程.
(2)从图象上看函数f(x)在x≤2时单调递增,只需使当x>2的函数f(x)=ax+a-1再单调递增即可,由于函数f(x)=ax+a-1的图象恒过点(-1,-1),结合图象约束a的取值即可.
| 1 |
| x |
(2)从图象上看函数f(x)在x≤2时单调递增,只需使当x>2的函数f(x)=ax+a-1再单调递增即可,由于函数f(x)=ax+a-1的图象恒过点(-1,-1),结合图象约束a的取值即可.
解答:
解:(1)当x≤1时,f(x)=-x2+2x-2,图象是抛物线的一部分;当1<x≤2时,f(x)=-
,图象是反比例函数图象的一部分;当a=1时,x>2时,函数f(x)=x+1-1=x,图象是y=x的图象的一部分,画出函数的图象如图所示,其中,M(-1,-1)、A(2,-
)
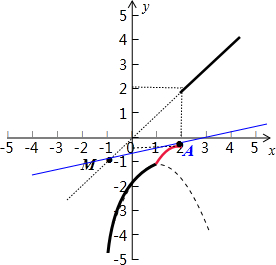
∵方程|f(x)|=5?f(x)=5或f(x)=-5
∴由图象可知,要使f(x)=5,则f(x)=x;要使f(x)=-5,则f(x)=-x2+2x-2;
原方程可化为x=5或-x2+2x-2=-5,
解得x=5或x=-1.
(2)当x>2时,f(x)=ax+a-1,由于f(-1)=-a+a-1=-1,
∴函数f(x)=ax+a-1的图象恒过点(-1,-1),且a为直线y=ax+a-1的斜率,
因此要使f(x)在(-∞,+∞)是单调递增的,斜率a≥kMA,其中kMA是直线MA的斜率,
∵kMA=
=
,∴a≥
| 1 |
| x |
| 1 |
| 2 |

∵方程|f(x)|=5?f(x)=5或f(x)=-5
∴由图象可知,要使f(x)=5,则f(x)=x;要使f(x)=-5,则f(x)=-x2+2x-2;
原方程可化为x=5或-x2+2x-2=-5,
解得x=5或x=-1.
(2)当x>2时,f(x)=ax+a-1,由于f(-1)=-a+a-1=-1,
∴函数f(x)=ax+a-1的图象恒过点(-1,-1),且a为直线y=ax+a-1的斜率,
因此要使f(x)在(-∞,+∞)是单调递增的,斜率a≥kMA,其中kMA是直线MA的斜率,
∵kMA=
-
| ||
| 2-(-1) |
| 1 |
| 6 |
| 1 |
| 6 |
点评:本题主要考查分段函数的内容,画出函数的图象,利用数形结合的数学思想是解决问题的关键.

练习册系列答案
相关题目
已知P={x|y=
},Q={y|y=
},则下列结论正确的是( )
| x-1 |
| x-1 |
| A、P=Q | B、P∪Q=R |
| C、P?Q | D、Q?P |
数列1,x,x2,…xn-1前n项的和Sn=( )
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |