题目内容
已知函数f(x)=
x3-
(a-3)x2-a(2a-3)x+b在(-1,1)上不单调,求实数a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:计算题,导数的概念及应用
分析:函数f(x)在区间(-1,1)上不单调?f'(x)=0在(-1,1)上有实根,且无重根,结合二次函数在(-1,1)上的图象求解.
解答:
解:∵f(x)=
x3-
(a-3)x2-a(2a-3)x+b,
∴f'(x)=x2-(a-3)x-a(2a-3)
若函数f(x)在(-1,1)上不单调,则方程f'(x)=0在(-1,1)上有实根,且无重根
由f'(x)=0,得x1=-a,x2=2a-3,
∴-1<-a<1或-1<2a-3<1,
∴-1<a<1或1<a<2,
又-a≠2a-3,∴a≠1.
∴实数a的取值范围为-1<a<1或1<a<2.
| 1 |
| 3 |
| 1 |
| 2 |
∴f'(x)=x2-(a-3)x-a(2a-3)
若函数f(x)在(-1,1)上不单调,则方程f'(x)=0在(-1,1)上有实根,且无重根
由f'(x)=0,得x1=-a,x2=2a-3,
∴-1<-a<1或-1<2a-3<1,
∴-1<a<1或1<a<2,
又-a≠2a-3,∴a≠1.
∴实数a的取值范围为-1<a<1或1<a<2.
点评:本题考查利用导数研究函数的单调性,函数f(x)在(-1,1)上不单调,则方程f'(x)=0在(-1,1)上有实根,且无重根,是解题的关键.

练习册系列答案
相关题目
函数y=|tan2x|是( )
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
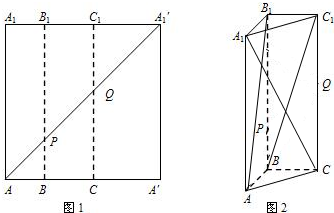 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.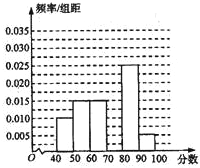 某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题: