题目内容
12.以原点为顶点,正半轴为对称轴的抛物线焦点在直线3x-4y=12上,则抛物线方程为y2=16x.分析 由已知直线方程求出直线与x轴正半轴的交点坐标,可得抛物线的焦点坐标,则抛物线方程可求.
解答 解:由3x-4y=12,得$\frac{x}{4}-\frac{y}{3}=1$,
∴直线3x-4y=12与x轴正半轴的交点坐标为(4,0),
即所求抛物线的焦点坐标为(4,0),
且由题意可知所求抛物线为开口向右的抛物线,
则其方程为y2=16x.
故答案为:y2=16x.
点评 本题考查抛物线方程的求法,关键是对题意的理解,是基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.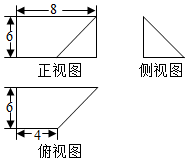 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |
7.下列函数中,既是偶函数又在区间(1,2)内单调递减的是( )
| A. | f(x)=-cosx | B. | f(x)=2x+2-x | C. | f(x)=$\frac{1}{{x}^{2}}$ | D. | f(x)=$\sqrt{-x}$ |
17.已知集合A={x|1<x<3},B={x|x2<4},则A∩B=( )
| A. | (-2,3) | B. | (1,2) | C. | (2,3) | D. | (2,4) |
1.已知复数z=a+bi(a,b∈R),则z∈R的充要条件是( )
| A. | a+bi=a-bi | B. | a+bi=-a+bi | C. | ab=0 | D. | a=b=0 |