题目内容
已知Rt△ABC中,AB=8,AC=4,BC=4
,则对于△ABC所在平面内的一点P,
•(
+
)的最小值是( )
| 3 |
| PA |
| PB |
| PC |
| A、-14 | B、-8 |
| C、-26 | D、-30 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:分别以CB,CA所在的直线为x,y轴建立直角坐标系,然后利用向量的数量积的坐标表示求解
•(
+
),根据两点间的距离公式即可求解
| PA |
| PB |
| PC |
解答:
解:分别以CB,CA所在的直线为x,y轴建立直角坐标系
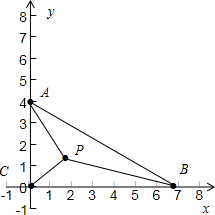
∵AB=8,AC=4
∴A(0,4),C(0,0),B(4
,0)
设P(x,y),则
=(-x,4-y),
=(4
-x,-y),
=(-x,-y),
∴
+
=(4
-2x,-2y)
∴
•(
+
)=[-x(4
-2x)]+(4-y)•(-2y)
=-4
x+2x2+2y2-8y
=2(x-
)2+2(y-2)2-14
即(x-
)2+(y-2)2为△ABC内一点到点(
,2)距离平方,当其最小时向量
•(
+
)的最小,
因为点(
,2)也在△ABC内,
所以(x-
)2+(y-2)2最小为0,所以
•(
+
)的最小值是-14.
故选:A.

∵AB=8,AC=4
∴A(0,4),C(0,0),B(4
| 3 |
设P(x,y),则
| PA |
| PB |
| 3 |
| PC |
∴
| PB |
| PC |
| 3 |
∴
| PA |
| PB |
| PC |
| 3 |
=-4
| 3 |
=2(x-
| 3 |
即(x-
| 3 |
| 3 |
| PA |
| PB |
| PC |
因为点(
| 3 |
所以(x-
| 3 |
| PA |
| PB |
| PC |
故选:A.
点评:本题主要考查了向量的数量积的坐标表示的应用,解题的关键是根据所求式子几何意义.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知集合A={y丨y=x2},B={x丨
<0},求A∩B=( )
| x+1 |
| x-2 |
| A、[0,+∞) |
| B、(-1,2) |
| C、[0,2) |
| D、(-1,0] |
将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
| A、4π | B、3π | C、2π | D、π |
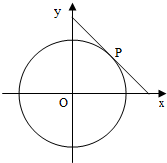 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图).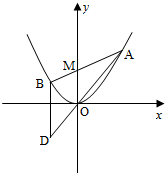 如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).
如图,已知抛物线C:x2=4y,过点M(0,2)任作一直线与C相交于A,B两点,过点B作y轴的平行线与直线AO相交于点D(O为坐标原点).