Question

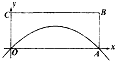为了测量抛物线y=x-x²与x轴所围成的封闭圆形面积，现截取矩形OABC，其中|OA|=1，|AB|=0.4，在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，据此可以估计封闭图形的面积为

 

．

Answer 1

考点：几何概型

专题：计算题,概率与统计

分析：先由试验估计，豆落在阴影部分的概率，再转化为几何概型的面积类型求解．

解答： 解：设封闭图形的面积为S，则
由题意，矩形OABC的面积为0.4，
∵在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，
∴

250

600

=

S

0.4

，
∴S=

1

6

．
故答案为：

1

6

．

点评：本题主要考查实验法求概率以及几何概型中面积类型，将两者建立关系，引入方程思想．