题目内容
设数列{an}是等差数列,且首项a1=3,a8-a3=10,Sn为数列前n项和.
(1)求数列{an}的通项公式及Sn;
(2)若数列{
}的前n项和为Tn,求Tn.
(1)求数列{an}的通项公式及Sn;
(2)若数列{
| 4 |
| an2-1 |
考点:数列的求和,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)利用“裂项求和”即可得出.
(2)利用“裂项求和”即可得出.
解答:
解:(1)设等差数列{an}的公差为d,
∵首项a1=3,a8-a3=10,
∴5d=10,解得d=2.
∴an=a1+(n-1)d=3+2(n-1)=2n+1.
Sn=
=n2+2n.
(2)∵
=
=
=
-
.
∴Tn=(1′-
)+(
-
)+…+(
-
)
=1-
=
.
∵首项a1=3,a8-a3=10,
∴5d=10,解得d=2.
∴an=a1+(n-1)d=3+2(n-1)=2n+1.
Sn=
| n(3+2n+1) |
| 2 |
(2)∵
| 4 | ||
|
| 4 |
| (2n+1)2-1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=(1′-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若θ∈(
,π),则
=( )
| π |
| 2 |
| 1-sin2θ |
| A、cosθ-sinθ |
| B、sinθ-cosθ |
| C、cosθ+sinθ |
| D、-cosθ-sinθ |
若命题“p∧q”为假,且“?q”为假,则( )
| A、“p∨q”为假 | B、p假 |
| C、p真 | D、不能判断q的真假 |
若m>0,0<n<1,则函数y=m+lognx的图象可能是( )
A、 |
B、 |
C、 |
D、 |
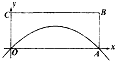 为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积,现截取矩形OABC,其中|OA|=1,|AB|=0.4,在该矩形内随机地撒600颗豆,数得落在该封闭圆形部分的豆数为250颗,据此可以估计封闭图形的面积为
为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积,现截取矩形OABC,其中|OA|=1,|AB|=0.4,在该矩形内随机地撒600颗豆,数得落在该封闭圆形部分的豆数为250颗,据此可以估计封闭图形的面积为