题目内容
已知α，β为锐角，且tan（2α+β）=
，tanα=
，（t∈[1，2]），求α+β的最大值．
| 3 |
| t |
| 1 |
| t |
考点：两角和与差的正切函数
专题：计算题,三角函数的求值
分析：由两角差的正切公式得到则tan（α+β）=tan[（2α+β）-α]=
，再由导数求出t+
的极小值点，也为最小值点，代入注意角的范围，即可得到最大值．
| 2 | ||
t+
|
| 3 |
| t |
解答：
解：由于α，β为锐角，且tan（2α+β）=
，tanα=
，
则tan（α+β）=tan[（2α+β）-α]=
=
=
，
由于1≤t≤2，则（t+
）′=1-
=0，则得t=
（负值舍去），
检验得t=
为极小值点，也为最小值点，
则有t+
的值域为[2
，4]，
则有tan（α+β）的最大值为
，
由于0＜α+β＜π，
即有α+β的最大值为
．
| 3 |
| t |
| 1 |
| t |
则tan（α+β）=tan[（2α+β）-α]=
| tan(2α+β)-tanα |
| 1+tan(2α+β)tanα |
| ||
1+
|
=
| 2 | ||
t+
|
由于1≤t≤2，则（t+
| 3 |
| t |
| 3 |
| t2 |
| 3 |
检验得t=
| 3 |
则有t+
| 3 |
| t |
| 3 |
则有tan（α+β）的最大值为
| ||
| 3 |
由于0＜α+β＜π，
即有α+β的最大值为
| π |
| 6 |
点评：本题考查三角函数的求值，考查两角差的正切函数的公式，考查函数的最值的求法，考查运算能力，属于中档题．
练习册系列答案
相关题目
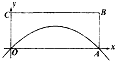为了测量抛物线y=x-x2与x轴所围成的封闭圆形面积，现截取矩形OABC，其中|OA|=1，|AB|=0.4，在该矩形内随机地撒600颗豆，数得落在该封闭圆形部分的豆数为250颗，据此可以估计封闭图形的面积为