题目内容
如图,在四棱锥P-ABCD中,AD⊥DB,其中三棱锥P-BCD的三视图如图所示,且sin∠BDC=

(I)求证:AD⊥PB;
(Ⅱ)若PA与平面PCD所成角的正弦值为
,求AD的长.
| 3 |
| 5 |

(I)求证:AD⊥PB;
(Ⅱ)若PA与平面PCD所成角的正弦值为
12
| ||
| 65 |
考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得AD⊥PD,AD⊥DB,从而AD⊥PD,又AD⊥DB,进而AD⊥平面PBD,由此能证明AD⊥PB.
(Ⅱ)以D为原点,以DA、DB、DP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出AD.
(Ⅱ)以D为原点,以DA、DB、DP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出AD.
解答:
(Ⅰ)证明:由三视图得PD⊥平面ABCD,
∵AD?平面ABCD,∴AD⊥PD,
又AD⊥DB,且PD∩BD=D,PD,BD?平面PBD,
∴AD⊥PD,又AD⊥DB,且PD∩BD=D,
PD、BD?平面PBD,
∴AD⊥平面PBD,
又PB?平面PBD,∴AD⊥PB.
(Ⅱ)解:由(Ⅰ)知,PD、AD、BD两两垂直,
以D为原点,以DA、DB、DP所在直线分别为x轴,y轴,z轴,
建立如图所求的空间直角坐标系,
设AD=λ,λ>0,结合sin∠BDC=
,得:
A(λ,0,0),B(0,3,0),C(-
,-
,0),P(0,0,4),
∴
=(λ,0,-4),
=(-
,
,0),
=(0,0,4),
设
=(x,y,z)为平面PCD的法向量,
由题意知
,
取y=3,得
=(4,3,0),
设PA与平面PCD所成角为θ,
∵PA与平面PCD所成角的正弦值为
,
∴sinθ=|cos<
,
>|=|
|=
,
解得λ=6,∴AD=6.
∵AD?平面ABCD,∴AD⊥PD,

又AD⊥DB,且PD∩BD=D,PD,BD?平面PBD,
∴AD⊥PD,又AD⊥DB,且PD∩BD=D,
PD、BD?平面PBD,
∴AD⊥平面PBD,
又PB?平面PBD,∴AD⊥PB.
(Ⅱ)解:由(Ⅰ)知,PD、AD、BD两两垂直,
以D为原点,以DA、DB、DP所在直线分别为x轴,y轴,z轴,
建立如图所求的空间直角坐标系,
设AD=λ,λ>0,结合sin∠BDC=
| 3 |
| 5 |
A(λ,0,0),B(0,3,0),C(-
| 9 |
| 5 |
| 12 |
| 5 |
∴
| PA |
| DC |
| 9 |
| 5 |
| 12 |
| 5 |
| DP |
设
| n |
由题意知
|
取y=3,得
| n |
设PA与平面PCD所成角为θ,
∵PA与平面PCD所成角的正弦值为
12
| ||
| 65 |
∴sinθ=|cos<
| PA |
| n |
| 4λ | ||
5
|
12
| ||
| 65 |
解得λ=6,∴AD=6.
点评:本题考查几何体的三视图、线面角的计算、线面、线线垂直的位置关系,考查空间想象能力以及论证推理能力.

练习册系列答案
相关题目
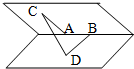 如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2
如图在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2| 17 |
| A、30° | B、60° |
| C、90° | D、120° |
已知P(-2,0)、Q(2,0)若点M是抛物线y2=4x上的动点,则
的最大值为( )
| |MP| |
| |MQ| |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
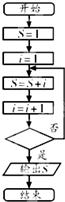 阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )
阅读如图所示的程序框图( 框图中的赋值符号“=”也可以写成“←”或“:=”),若输出S的值等于7,那么在程序框图中的判断框内应填写的条件是( )| A、i>2? | B、i>3? |
| C、i>4? | D、i>5? |
 在长方体ABCDA1B1C1D1中,E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点.求证:平面A1EFD1∥平面BCF1E1.
在长方体ABCDA1B1C1D1中,E、F、E1、F1分别是AB、CD、A1B1、C1D1的中点.求证:平面A1EFD1∥平面BCF1E1.