Question

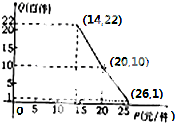甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙，并约定从该店经营的利润中，逐步偿还转让费（不计息），直到还清．已知：①这种消费品的进价每件14元；②该店月销量Q（百件）与销售单价P（元/件）的关系如图所示的折线段；③该店每月需各种开支2000元．
（Ⅰ）写出月销量Q（百件）与销售单价P（元/件）的关系，并求该店的月利润L（元）关于销售单价P（元/件）的函数关系式（该店的月利润=月销售利润-该店每月支出，不包括转让费及贷款）；
（Ⅱ）当商品的价格为每件多少元时，该店的利润最大？并求该店的月利润的最大值；
（Ⅲ）若乙只依靠该店，最早可望在多少年后无债务？

Answer 1

考点：分段函数的应用,函数模型的选择与应用

专题：计算题,应用题,函数的性质及应用

分析：（Ⅰ）运用分段函数的形式写出Q的表达式，再由L=Q（P-14）×100-2000，写出L的分段函数形式；
（Ⅱ）分别求出各段的最大值，比较即可得到最大值；
（Ⅲ）设可在n年后脱贫（无债务），依题意有，12n×4050-572000-400000≥0，解出即可．

解答： 解：（Ⅰ）Q=

-2P+50，14≤P≤20 - 3 2 P+40，20＜P≤26

，
则L=Q（P-14）×100-2000
因此，L=

(50-2P)(P-14)×100-2000，14≤P≤20 (40- 3 2 P)(P-14)×100-2000，20＜P≤26

．
（Ⅱ）当14≤P≤20时，L=-2（P-

39

2

）²+4050，
则当p=

39

2

时，L_max=4050；
当20＜P≤26时，L=-

3

2

（x-

61

3

）²+4016

2

3

，
当x=

61

3

时，L_max=4016

2

3

，
由于4050＞4016

2

3

，所以当P=19.5元时，月利润最大，为4050元；
（Ⅲ）设可在n年后脱贫（无债务），
依题意有，12n×4050-572000-400000≥0，
解得n≥20，
即最早在20年后无债务．

点评：本题考查分段函数及运用，考查分段函数的最值，应考虑各段的最值，考查运算能力，属于中档题．