题目内容
已知等差数列{an}的前n项和Sn,且am-1+am+1-2am2=0,S2m-1=19,则m= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由题意和等差数列的性质可得am=0,或am=1,再由求和公式和性质可得=(2m-1)am=19,可得am=1,m=10
解答:
解:∵am-1+am+1-2am2=0,
∴由等差数列的性质可得2am-2am2=0,
解得am=0,或am=1,
又S2m-1=
=
=(2m-1)am=19,
∴am=1,m=10
故答案为:10
∴由等差数列的性质可得2am-2am2=0,
解得am=0,或am=1,
又S2m-1=
| (2m-1)(a1+a2m-1) |
| 2 |
=
| (2m-1)•2am |
| 2 |
∴am=1,m=10
故答案为:10
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
相关题目
已知集合A={x|y=log2(x2-1)},B={y|y=(
)x-1},则A∩B等于( )
| 1 |
| 2 |
A、{x|
| ||
| B、{x|1<x<2} | ||
| C、{x|x>0} | ||
| D、{x|x>1} |
设a=log23,b=(
)3,c=sin90°,则( )
| 1 |
| 2 |
| A、a<c<b |
| B、b<c<a |
| C、c<a<b |
| D、c<b<a |
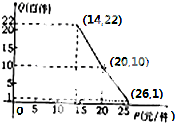 甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.
甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.