题目内容
数列{an}的前n项和Sn=4an-3.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn+1=an+bn,且b1=2,求{bn}的通项公式.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足bn+1=an+bn,且b1=2,求{bn}的通项公式.
考点:数列递推式
专题:等差数列与等比数列
分析:(1)由已知得a1=S1=4a1-3,an=Sn-Sn-1=4an-3-4an-1+3(n>1)=4(an-an-1),由此能求出{an}的通项公式an=(
)n-1.
(2)由已知得an=bn+1-bn,从而
ak=
(bk+1-bk)=bn-b1(n≥2),由此能求出{bn} 的通项公式bn=3(
)n-1-1.
| 4 |
| 3 |
(2)由已知得an=bn+1-bn,从而
| n-1 |
 |
| k=1 |
| n-1 |
 |
| k=1 |
| 4 |
| 3 |
解答:
解:(1)a1=S1=4a1-3
∴a1=1
an=Sn-Sn-1=4an-3-4an-1+3(n>1)
=4(an-an-1)
an=
an-1,∴{an}为q=
的等比数列,
∴{an}的通项公式an=(
)n-1.
(2)∵bn+1=an+bn,
∴an=bn+1-bn,
∴
ak=
(bk+1-bk)=bn-b1(n≥2),
∴bn=b1+
ak=2+
=3(
)n-1-1,n≥2,
∵b1=2=3(
)1-1-1,
∴{bn} 的通项公式bn=3(
)n-1-1.
∴a1=1
an=Sn-Sn-1=4an-3-4an-1+3(n>1)
=4(an-an-1)
an=
| 4 |
| 3 |
| 4 |
| 3 |
∴{an}的通项公式an=(
| 4 |
| 3 |
(2)∵bn+1=an+bn,
∴an=bn+1-bn,
∴
| n-1 |
 |
| k=1 |
| n-1 |
 |
| k=1 |
∴bn=b1+
| n-1 |
 |
| k=1 |
1-(
| ||
1-
|
| 4 |
| 3 |
∵b1=2=3(
| 4 |
| 3 |
∴{bn} 的通项公式bn=3(
| 4 |
| 3 |
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
函数y=
的值域是( )
| 16-4x |
| A、[0,+∞) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
如果执行图中的程序框图,那么输出的n为( )


| A、5 | B、6 | C、7 | D、8 |
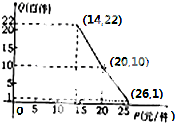 甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.
甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.