题目内容
已知函数f(x)=2x
(1)写出函数f(x)的反函数g(x)及定义域;
(2)借助计算器用二分法求g(x)=4-x的近似解(精确度0.1)
(1)写出函数f(x)的反函数g(x)及定义域;
(2)借助计算器用二分法求g(x)=4-x的近似解(精确度0.1)
考点:反函数,二分法求方程的近似解
专题:计算题,函数的性质及应用
分析:(1)运用指数式和对数式的互化,即可得到反函数,并由对数函数的定义域即可得到所求的定义域;
(2)令h(x)=log2x-4+x,由于h(2)<0,h(3)>0,则h(x)=0的解在(2,3),则分别取4次的中点,计算函数值,由零点存在定理,即可判断零点的近似解.
(2)令h(x)=log2x-4+x,由于h(2)<0,h(3)>0,则h(x)=0的解在(2,3),则分别取4次的中点,计算函数值,由零点存在定理,即可判断零点的近似解.
解答:
解:(1)函数y=f(x)=2x,即有x=log2y,
则函数f(x)的反函数g(x)=log2x,定义域为(0,+∞);
(2)g(x)=4-x即log2x=4-x,
令h(x)=log2x-4+x,由于h(2)<0,h(3)>0,
则h(x)=0的解在(2,3),则取x1=2.5,h(2.5)<0,
则解在(2.5,3)上,则取x2=2.75,h(2.75)>0,
则解在(2.5,2.75)上,则取x3=2.625,h(2.625)>0,
则解在(2.5,2.625)上,则取x4=2.5625,h(2.5625)<0,
则解在(2.5625,2.625)之间,
故近似解为2.6.
则函数f(x)的反函数g(x)=log2x,定义域为(0,+∞);
(2)g(x)=4-x即log2x=4-x,
令h(x)=log2x-4+x,由于h(2)<0,h(3)>0,
则h(x)=0的解在(2,3),则取x1=2.5,h(2.5)<0,
则解在(2.5,3)上,则取x2=2.75,h(2.75)>0,
则解在(2.5,2.75)上,则取x3=2.625,h(2.625)>0,
则解在(2.5,2.625)上,则取x4=2.5625,h(2.5625)<0,
则解在(2.5625,2.625)之间,
故近似解为2.6.
点评:本题主要考查函数的反函数和用二分法求方程的近似解的方法和步骤,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
某设备的使用年限x与所支出的总费用y(万元)统计数据如下表
据上表可得回归方程
=
x+
中的
=0.7,据此预测设备使用年限为6年时总费用为( )
| 使用年限x | 1 | 2 | 3 | 4 |
| 总费用y | 1.5 | 2 | 3 | 3.5 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、4.95万元 |
| B、5.2万元 |
| C、4.35万元 |
| D、4.9万元 |
函数f(x)=ax-1(a>0,且a≠1)的图象一定过定点( )
| A、(0,1) |
| B、(1,1) |
| C、(1,0) |
| D、(0,0) |
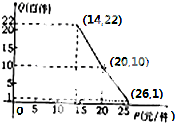 甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.
甲将经营的某淘宝店以57.2万元的优惠价格转让给了尚有40万元无息贷款没有偿还的乙,并约定从该店经营的利润中,逐步偿还转让费(不计息),直到还清.已知:①这种消费品的进价每件14元;②该店月销量Q(百件)与销售单价P(元/件)的关系如图所示的折线段;③该店每月需各种开支2000元.