题目内容
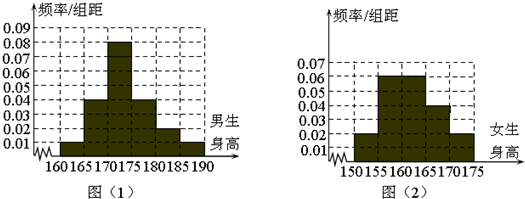
某学校为调查高二年级学生的身高情况,按随机抽样的方法抽取200名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有48人.
(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高.
(Ⅱ)在上述200名学生中,从身高在170~175cm之间的学生按男、女性别分层抽样的方法,抽出7人,从这7人中选派4人当旗手,求4人中至少有一名女生的概率.

(Ⅰ)在抽取的学生中,身高不超过165cm的男、女生各有多少人?并估计男生的平均身高.
(Ⅱ)在上述200名学生中,从身高在170~175cm之间的学生按男、女性别分层抽样的方法,抽出7人,从这7人中选派4人当旗手,求4人中至少有一名女生的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(I)由图(1)知:身高在170~175cm的男生的频率为0.08×5=0.4,进而点到男生总人数与女生总人数,根据身高不超过165cm的男生女生的频率即可得出人数,取男生的每一组的中点乘以人数的和即可得出平均身高.
(II)分别计算出身高在170~175cm之间的学生按男生女生人数,按比例得出抽出7人中,有6个男生,1个女生,而这7人中选派4人当旗手的方法数共有
(种),4人中至少有一名女生的方法数为
(种),利用古典概型的概率计算公式即可得出.
(II)分别计算出身高在170~175cm之间的学生按男生女生人数,按比例得出抽出7人中,有6个男生,1个女生,而这7人中选派4人当旗手的方法数共有
| ∁ | 4 7 |
| ∁ | 3 6 |
解答:
解:(I)由图(1)知:身高在170~175cm的男生的频率为0.08×5=0.4,
设男生总人数为m,则m×0.4=48,∴m=120(人),
∴女生总人数为200-120=80(人),
∴身高不超过165cm的男生有120×0.01×5=6(人),
身高不超过165cm的女生有80×(0.02+0.06+0.06)×5=56(人),
男生的平均身高为:162.5×0.01×5+167.5×0.04×5+172.5×0.08×5+177.5×0.04×5
+182.5×0.02×5+187.5×0.01×5=173.75(cm).
(II)身高在170~175cm之间的学生按男生为120×0.08×5=48(人),
身高在170~175cm之间的学生按女生为80×0.02×5=8(人),
∵48:8=6:1,∴抽出7人中,有6个男生,1个女生,
∴这7人中选派4人当旗手的方法数共有
=35(种),
4人中至少有一名女生的方法数为
=20(种),
∴4人中至少有一名女生的概率为p=
=
.
设男生总人数为m,则m×0.4=48,∴m=120(人),
∴女生总人数为200-120=80(人),
∴身高不超过165cm的男生有120×0.01×5=6(人),
身高不超过165cm的女生有80×(0.02+0.06+0.06)×5=56(人),
男生的平均身高为:162.5×0.01×5+167.5×0.04×5+172.5×0.08×5+177.5×0.04×5
+182.5×0.02×5+187.5×0.01×5=173.75(cm).
(II)身高在170~175cm之间的学生按男生为120×0.08×5=48(人),
身高在170~175cm之间的学生按女生为80×0.02×5=8(人),
∵48:8=6:1,∴抽出7人中,有6个男生,1个女生,
∴这7人中选派4人当旗手的方法数共有
| C | 4 7 |
4人中至少有一名女生的方法数为
| C | 3 6 |
∴4人中至少有一名女生的概率为p=
| 20 |
| 35 |
| 4 |
| 7 |
点评:本题考查了频率分布直方图的有关知识与计算、古典概型的概率计算公式,考查了学会看图及用图,考查了计算能力,属于中档题.

练习册系列答案
相关题目
设函数f(x)=xlnx,则( )
| A、x=1为f(x)的极大值点 | ||
| B、x=1为f(x)的极小值点 | ||
C、x=
| ||
D、x=
|
连续函数y=f(x)在点x0取极值是f′(x0)=0的( )
| A、充分条件 | B、必要条件 |
| C、充要条件 | D、必要非充分条件 |