题目内容
已知f(x)为奇函数,当x∈[0,2]时,f(x)=-x2+2x;当x∈(2,+∞)时,f(x)=2x-4,若关于x的不等式f(x+a)>f(x)有解,则a的取值范围为 .
考点:函数单调性的性质
专题:综合题,函数的性质及应用
分析:根据题意画出函数f(x)的图象,根据图象及函数f(x)的单调性,f(x+a),和f(x)的取值即可找出a的范围.
解答:
解:由题意作出函数f(x)的图象,如图所示: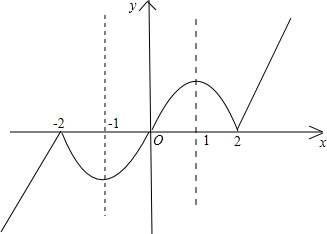 若a>0,则x≥2时,x+a>2,x+a>x;
若a>0,则x≥2时,x+a>2,x+a>x;
f(x)在[2,+∞)上单调递增,所以f(x+a)>f(x),即该不等式有解;
若a<0,x+a<x,若x≥2,则x+a≥2+a,要使不等式f(x+a)>f(x)有解,需2+a>0,即a>-2;
若0≤x<2,则a≤x+a<2+a,则需2+a>0,即a>-2时,f(x+a)>f(x)有解;
若-2<x<0,-2+a<x+a<a,则需a>-2,不等式f(x+a)>f(x)有解;
若x≤-2,x+a≤a-2<-2,函数f(x)在(-∞,-2]为增函数,所以f(x+a)<f(x),即不等式f(x+a)>f(x)无解;
综上得a的取值范围是(-2,0∪(0,+∞).
故答案为:(-2,0)∪(0,+∞).
 若a>0,则x≥2时,x+a>2,x+a>x;
若a>0,则x≥2时,x+a>2,x+a>x;f(x)在[2,+∞)上单调递增,所以f(x+a)>f(x),即该不等式有解;
若a<0,x+a<x,若x≥2,则x+a≥2+a,要使不等式f(x+a)>f(x)有解,需2+a>0,即a>-2;
若0≤x<2,则a≤x+a<2+a,则需2+a>0,即a>-2时,f(x+a)>f(x)有解;
若-2<x<0,-2+a<x+a<a,则需a>-2,不等式f(x+a)>f(x)有解;
若x≤-2,x+a≤a-2<-2,函数f(x)在(-∞,-2]为增函数,所以f(x+a)<f(x),即不等式f(x+a)>f(x)无解;
综上得a的取值范围是(-2,0∪(0,+∞).
故答案为:(-2,0)∪(0,+∞).
点评:考查奇函数的概念,二次函数图象,奇函数图象关于原点的对称性,以及函数单调性的定义.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
函数y=
+
的定义域是( )
|
| 9-x |
A、(-
| ||
B、(-
| ||
C、[-
| ||
D、[-
|
在△ABC中,角A,B,C的对边分别是a,b,c,若∠A:∠B=1:1,a:c=2:3则cos2A的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设[x]表示不大于x的最大整数,则对任意实数x,有( )
| A、[-x]=-[x] | ||
B、[x+
| ||
| C、[2x]=2[x] | ||
D、[x]+[x+
|
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A、(-1,+∞) |
| B、(-∞,-1) |
| C、(2,+∞) |
| D、(-∞,-2) |
 如图,在三棱锥 S-ABC中,AC⊥SA,AC⊥AB,SA=SB=AB=2,AC=1.
如图,在三棱锥 S-ABC中,AC⊥SA,AC⊥AB,SA=SB=AB=2,AC=1. 为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00 间各自的点击量,得如图所示的统计图,根据统计图:
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00-10:00 间各自的点击量,得如图所示的统计图,根据统计图: