Question

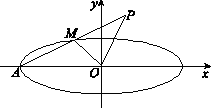如图，椭圆C：

x2

4

+

y2

m

=1（0＜m＜4）的左顶点为A，M是椭圆C上异于点A的任意一点，点P与点A关于点M对称．
（1）若点P的坐标为（4，3），求m的值；
（2）若椭圆C上存在点M，使得OP⊥OM，求实数m的最大值．

Answer 1

考点：直线与圆锥曲线的关系,基本不等式在最值问题中的应用,椭圆的标准方程

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）依题意，M是线段AP的中点，求出M的坐标，代入椭圆方程，即可求m的值；
（2）设M（x₀，y₀），则

x 2 0

4

+

y 2 0

m

=1，因为OP⊥OM，所以x0(2x0+2)+2y02=0．两式联立，表示出m，利用基本不等式即可得出结论．

解答： 解：（1）依题意，M是线段AP的中点，
因为A（-2，0），P（4，3），
所以点M的坐标为(1，

3

2

)．
由点M在椭圆C上，所以

1

4

+

9

4m

=1，
解得m=3．
（2）设M（x₀，y₀），则

x 2 0

4

+

y 2 0

m

=1①，由题意知-2＜x₀＜2．
因为M是线段AP的中点，所以P（2x₀+2，2y₀）．
因为OP⊥OM，所以x0(2x0+2)+2y02=0．②
由①②消去y₀，整理可得m=

4x0(x0+1)

x02-4

=4+

4

(x0+4)+ 12 x0+4 -8

≤2-

3

，
当且仅当x₀=-4+2

3

时，等号成立，
因为0＜m＜4，
所以m的最大值是2-

3

．

点评：本题考查椭圆方程，考查基本不等式的运用，考查学生分析解决问题的能力，正确表示点的坐标是关键．