题目内容
已知{an}是正数组成的数列，a1=1，且点(
，an+1)（n∈N*）在函数y=x2+1的图象上．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=1，bn+1=bn+2an，求数列{bn}的通项．
| an |
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足b1=1，bn+1=bn+2an，求数列{bn}的通项．
考点：数列递推式
专题：计算题,点列、递归数列与数学归纳法
分析：（Ⅰ）由已知得an+1-an=1，a1=1，所以数列{an}是以1为首项，公差为1的等差数列，由此能求出an；
（Ⅱ）bn+1-bn=2n，bn=（bn-bn-1）+（bn-1-bn-2）+…+（b2-b1）+b1=2n-1+2n-2+…+23+21+1，利用等比数列的求和公式，即可求出数列{bn}的通项公式．
（Ⅱ）bn+1-bn=2n，bn=（bn-bn-1）+（bn-1-bn-2）+…+（b2-b1）+b1=2n-1+2n-2+…+23+21+1，利用等比数列的求和公式，即可求出数列{bn}的通项公式．
解答：
解：（Ⅰ）由已知得an+1=an+1，
即an+1-an=1．
又a1=1，所以数列{an}是以1为首项，公差为1的等差数列，
故an=1+（n-1）×1=n；
（Ⅱ）由（Ⅰ）知an=n，从而bn+1-bn=2n，
bn=（bn-bn-1）+（bn-1-bn-2）+…+（b2-b1）+b1=2n-1+2n-2+…+23+21+1=
=2n-1．
即an+1-an=1．
又a1=1，所以数列{an}是以1为首项，公差为1的等差数列，
故an=1+（n-1）×1=n；
（Ⅱ）由（Ⅰ）知an=n，从而bn+1-bn=2n，
bn=（bn-bn-1）+（bn-1-bn-2）+…+（b2-b1）+b1=2n-1+2n-2+…+23+21+1=
| 1-2n |
| 1-2 |
点评：本题考查了等差数列的通项公式，考查了数列的函数特性，此题为中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若P是平面外一点，A为平面内一点，
为平面的一个法向量，则点P到平面的距离是（ ）
| n |
A、|
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
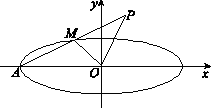如图，椭圆C：