题目内容

已知函数f（x）=x|x-a|，（a∈R），若a=2，解关于x的不等式f（x）＜x．
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：当a=2时，不等式f（x）＜x?x|x-2|＜x，对x分x＞0与x＜0讨论，解简单的绝对值不等式即可．
解答： 解：当a=2时，不等式f（x）＜x即x|x-2|＜x，
显然x≠0，
当x＞0时，原不等式可化为：|x-2|＜1⇒-1＜x-2＜1⇒1＜x＜3；
当x＜0时，原不等式可化为：|x-2|＞1⇒x-2＞1或x-2＜-1⇒x＞3或x＜1
∴x＜0；
综上得：当a=2时，原不等式的解集为{x|1＜x＜3或x＜0}．
点评：本题考查绝对值不等式的解法，对x分x＞0与x＜0讨论是关键，考查分类讨论思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
已知直角坐标系xoy中，直线l的参数方程为
x=t-3 
y=
3
t 
(t为参数)．以直角坐标系xoy中的原点O为极点，x轴的非负半轴为极轴，圆C的极坐标方程为ρ2-4ρcosθ+3=0．
①求直线l与圆C的直角坐标方程；   
②判断直线l与圆C的位置关系．
如图，椭圆C：
x2
4
+
y2
m
=1（0＜m＜4）的左顶点为A，M是椭圆C上异于点A的任意一点，点P与点A关于点M对称．
（1）若点P的坐标为（4，3），求m的值；
（2）若椭圆C上存在点M，使得OP⊥OM，求实数m的最大值．
已知f（x+2）的定义域为[1，2]，求f（2x+1）的定义域．
已知函数f（x）=x2+ax+3，g（x）=（6+a）•2x-1
（Ⅰ）若f（1）=f（3），求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，判断函数F（x）=
2
1+g(x)
的单调性，并给出证明；
（Ⅲ）当x∈[-2，2]时，f（x）≥a（a∉（-4，4））恒成立，求实数a的最小值．
已知
tanα
1-tanα
=-
1
3

（Ⅰ）求
sinα-2cosα
3sinα+cosα
的值；
（Ⅱ）若α∈(0，π)，β∈(0，
π
2
)，cos(2β+α)=
5
5
，求sinβ的值．
某商店经销一种商品，每件进价7元，市场预计以每件20元的价格销售时该店一年可销售2000件，经过市场调研发现每件销售价格在每件20元的基础上每减少一元则增加销售400件，而每增加一元则减少销售100件，现设每件的销售价格为x元，x为整数．
（Ⅰ）写出该商店一年内销售这种商品所获利润y（元）与每件的销售价格x（元）的函数关系式（并写出这个函数的定义域）；
（Ⅱ）当每件销售价格x为多少元时，该商店一年内利润y（元）最大，并求出最大值．
函数y=
2x-4
的定义域为
 
．
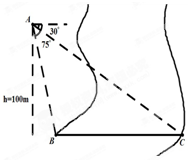如图，在气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，若此时的气球高度是100m，则河流在B，C两地的宽度为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网