题目内容
【选修4-4:坐标系与参数方程】
在直角坐标系xOy中,直线l的参数方程为
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为ρ=
cos(θ+
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
在直角坐标系xOy中,直线l的参数方程为
|
| 2 |
| π |
| 4 |
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)求直线l被曲线C所截得的弦长.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:本题的关键(1)是直线l的参数方程为
(t为参数)和曲线C的极坐标方程为ρ=
cos(θ+
)的普通方程的转化,(2)是借助垂径定理,求解弦长问题.
|
| 2 |
| π |
| 4 |
解答:
解:(1)∵直线l的参数方程为
(t为参数),(t为参数)
∴化为普通方程为l:3x+4y+1=0.
又∵曲线C的极方程为ρ=
cos(θ+
),
∴化为直角坐标方程为x2+y2-x+y=0.
(2)由(1)可知曲线C表示圆心为(
,-
),半径为
的圆,
∴则圆心到直线l的距离d═
=
,
∴直线l被曲线C截得的弦长为2
=2
=
|
∴化为普通方程为l:3x+4y+1=0.
又∵曲线C的极方程为ρ=
| 2 |
| π |
| 4 |
∴化为直角坐标方程为x2+y2-x+y=0.
(2)由(1)可知曲线C表示圆心为(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴则圆心到直线l的距离d═
|
| ||
|
| 1 |
| 10 |
∴直线l被曲线C截得的弦长为2
| r2-d2 |
|
| 7 |
| 5 |
点评:此题考查参数方程和极坐标方程化为普通方程,是一道高考常见的题目

练习册系列答案
相关题目
M={x|x<2或x≥3},N={x|2<x<4},则(∁RM)∩N=( )
| A、{x|2≤x<3} |
| B、{x|2<x≤3} |
| C、{x|2<x<3} |
| D、{x|3≤x<4} |
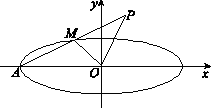 如图,椭圆C:
如图,椭圆C: