题目内容
若a+b+c=1，a，b，c∈R+，
+
+
≤m，则m最小值是 ．
| 4a+1 |
| 4b+1 |
| 4c+1 |
考点：基本不等式
专题：不等式的解法及应用
分析：利用柯西不等式即可得出．
解答：
解：∵1•
+1•
+1•
≤
•
=
，
当且仅当a=b=c=
时取等号，∴
+
+
的最大值为
．
∴m≥(
+
+
)max=
．
故m的最小值是
．
故答案为：
．
| 4a+1 |
| 4b+1 |
| 4c+1 |
| 1+1+1 |
| 4a+1+4b+1+4c+1 |
| 21 |
当且仅当a=b=c=
| 1 |
| 3 |
| 4a+1 |
| 4b+1 |
| 4c+1 |
| 21 |
∴m≥(
| 4a+1 |
| 4b+1 |
| 4c+1 |
| 21 |
故m的最小值是
| 21 |
故答案为：
| 21 |
点评：本题考查了柯西不等式，属于基础题．
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
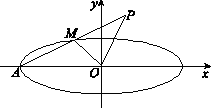如图，椭圆C：
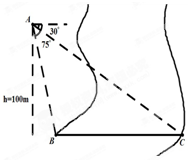如图，在气球A上测得正前方的河流的两岸B，C的俯角分别为75°，30°，若此时的气球高度是100m，则河流在B，C两地的宽度为