题目内容
已知函数f(x)=x2-1,证明函数f(x)在(-∞,0)的单调性.
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数单调性的定义即可得到结论.
解答:
证明:设x1<x2<0,
则f(x1)-f(x2)=
-1-
+1=
-
=(x1+x2)(x1-x2),
∵x1<x2<0,
∴x1+x2<0,x1-x2<0,
即f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(-∞,0)的单调递减.
则f(x1)-f(x2)=
| x | 2 1 |
| x | 2 2 |
| x | 2 1 |
| x | 2 2 |
∵x1<x2<0,
∴x1+x2<0,x1-x2<0,
即f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(-∞,0)的单调递减.
点评:本题主要考查函数单调性的判断和证明,利用单调性的定义是解决本题的关键.

练习册系列答案
相关题目
复数z=1+i(i为虚数单位),则复数z的共轭复数的模|
|=( )
. |
| z |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若P是平面外一点,A为平面内一点,
为平面的一个法向量,则点P到平面的距离是( )
| n |
A、|
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
M={x|x<2或x≥3},N={x|2<x<4},则(∁RM)∩N=( )
| A、{x|2≤x<3} |
| B、{x|2<x≤3} |
| C、{x|2<x<3} |
| D、{x|3≤x<4} |
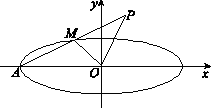 如图,椭圆C:
如图,椭圆C: