题目内容
解关于x的不等式
>0(a≥0)
| ax-1 |
| x2-x-2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:不等式等价于(ax-1)(x+1)(x-2)>0,再分当a=0时、当a>0时、当a=
时、当0<
<
时、当a>
时五种情况,分别求得不等式的解集.
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:原不等式等价于(ax-1)(x+1)(x-2)>0,
当a=0时,原不等式等价于(x-2)(x+1)<0,解得-1<x<2,
此时原不等式得解集为{x|-1<x<2};
当a>0时,原不等式等价于(x-
)(x+1)(x-2)>0,
当a=
时,原不等式的解集为 {x|x>-1,且 x≠2};
当0<
<
时,不等式的解集为{x|x>
,或-1<x<2 };
当a>
时,原不等式的解集为{x|-1<x<
,或x>2}.
当a=0时,原不等式等价于(x-2)(x+1)<0,解得-1<x<2,
此时原不等式得解集为{x|-1<x<2};
当a>0时,原不等式等价于(x-
| 1 |
| a |
当a=
| 1 |
| 2 |
当0<
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
当a>
| 1 |
| 2 |
| 1 |
| a |
点评:本题主要考查分式不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
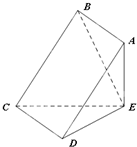 如图,E是平面ABCD外一点,AE⊥平面CDE.若四边形ABCD是正方形,M,N分别是AE,BC的中点.
如图,E是平面ABCD外一点,AE⊥平面CDE.若四边形ABCD是正方形,M,N分别是AE,BC的中点.