题目内容
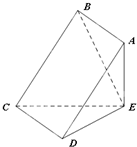 如图,E是平面ABCD外一点,AE⊥平面CDE.若四边形ABCD是正方形,M,N分别是AE,BC的中点.
如图,E是平面ABCD外一点,AE⊥平面CDE.若四边形ABCD是正方形,M,N分别是AE,BC的中点.(Ⅰ)求证:平面ABCD⊥平面ADE;
(Ⅱ)求证:MN∥平面CDE;
(Ⅲ)若二面角B-CD-E的平面角的大小为30°,求BD与平面AEC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)先根据线面垂直的判定定理证明出CD⊥平面ADE,进而根据面面垂直的判定证明出平面ABCD⊥平面ADE.
(2)作AD的中点F,连结NF,MF,先证明出平面MNF∥平面CDE,进而根据面面平行的性质证明出MN∥平面CDE.
(3)过D作DG⊥CE,连结BD交AC于O,连结OG,作出所求二面角的平面角,进而根据已知条件求得CE,DG,OD,求得答案.
(2)作AD的中点F,连结NF,MF,先证明出平面MNF∥平面CDE,进而根据面面平行的性质证明出MN∥平面CDE.
(3)过D作DG⊥CE,连结BD交AC于O,连结OG,作出所求二面角的平面角,进而根据已知条件求得CE,DG,OD,求得答案.
解答:
(1)证明:∵AE⊥平面CDE,CD?平面CDE,
∴AE⊥CD,
∵四边形ABCD是正方形,
∴CD⊥AD,
∵AD∩AE=A,AD?平面ADE,AE?平面ADE,
∴CD⊥平面ADE,
∵CD?平面ABCD,
∴平面ABCD⊥平面ADE.
(2)作AD的中点F,连结NF,MF,
则NF∥CD,MF∥DE,
∵NF?平面CDE,MF?平面CDE,CD?平面CDE,MF平面CDE,
∴NF∥平面CDE,MF平面CDE,
∵NF=MF=F,NF?平面MNF,MF?平面MNF,
∴平面MNF∥平面CDE,
∵MN?平面MNF,
∴MN∥平面CDE.
(3)由(1)知CD⊥AD,CD⊥DE,
∴∠ADE为二面角B-CD-E的平面角,即∠ADE=30°,
设AD=2,则AE=1,DE=
,
过D作DG⊥CE,连结BD交AC于O,连结OG,
∵AE⊥平面CDE,DG?平面CDE,
∴DG⊥AE,
∵AE∩CE=E,AE?平面ACE,CE?平面ACE,
∴DG⊥平面ACE,
∵四边形ABCD是正方形,
∴AC⊥BD,
∵DG⊥平面ACE,
∴OG⊥AC,
∴∠GOD为BD与平面AEC所成角的平面角,
CE=
=
,
DG=
=
,OD=
=
,
∴sin∠GOD=
=
=
.

∴AE⊥CD,
∵四边形ABCD是正方形,
∴CD⊥AD,
∵AD∩AE=A,AD?平面ADE,AE?平面ADE,
∴CD⊥平面ADE,
∵CD?平面ABCD,
∴平面ABCD⊥平面ADE.
(2)作AD的中点F,连结NF,MF,
则NF∥CD,MF∥DE,
∵NF?平面CDE,MF?平面CDE,CD?平面CDE,MF平面CDE,
∴NF∥平面CDE,MF平面CDE,
∵NF=MF=F,NF?平面MNF,MF?平面MNF,
∴平面MNF∥平面CDE,
∵MN?平面MNF,
∴MN∥平面CDE.
(3)由(1)知CD⊥AD,CD⊥DE,
∴∠ADE为二面角B-CD-E的平面角,即∠ADE=30°,
设AD=2,则AE=1,DE=
| 3 |
过D作DG⊥CE,连结BD交AC于O,连结OG,
∵AE⊥平面CDE,DG?平面CDE,
∴DG⊥AE,
∵AE∩CE=E,AE?平面ACE,CE?平面ACE,
∴DG⊥平面ACE,
∵四边形ABCD是正方形,
∴AC⊥BD,
∵DG⊥平面ACE,
∴OG⊥AC,
∴∠GOD为BD与平面AEC所成角的平面角,
CE=
| 3+4 |
| 7 |
DG=
| CD•DE |
| CE |
2•
| ||
|
| BD |
| 2 |
| 2 |
∴sin∠GOD=
| DG |
| OD |
2
| ||||
|
| ||
| 7 |

点评:本题主要考查了线面平行,面面垂直的判定,及直线与平面所成的角,面面成角的计算.考查了学生空间观察能力和计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
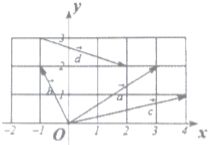 如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.
如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底. 如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.
如图,已知抛物线C的顶点在原点,开口向右,过焦点且垂直于抛物线对称轴的弦长为2,过C上一点A作两条互相垂直的直线交抛物线于P,Q两点.