题目内容
设数列{a2n-1}是公差为2的等差数列,数列{a2n}是公比为3的等比数列,数列{an}的前n项和为Sn(n∈N*),已知S3=a4,a3+a5=a4+2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若当n∈N*时,不等式2S2n-na2n-1<λa2n恒成立,求实数λ的取值范围.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若当n∈N*时,不等式2S2n-na2n-1<λa2n恒成立,求实数λ的取值范围.
考点:数列与不等式的综合,等差数列的通项公式,等比数列的通项公式
专题:点列、递归数列与数学归纳法,不等式的解法及应用
分析:(Ⅰ)把已知条件化为a1和a2的等式,联立后求解a1和a2,然后分别有等差数列和等比数列的通项公式求得数列{an}的通项公式;
(Ⅱ)利用分组求和求出S2n,结合2S2n-na2n-1<λa2n恒成立分离参数λ,然后构造辅助函数bn=
,由单调性得到bn的最大值,则实数λ的取值范围可求.
(Ⅱ)利用分组求和求出S2n,结合2S2n-na2n-1<λa2n恒成立分离参数λ,然后构造辅助函数bn=
| n-2 |
| 2×3n-1 |
解答:
解:(Ⅰ)由S3=a4,得a1+a2+a1+2=3a2,即a1+1=a2 ①
由a3+a5=a4+2,得a1+2+a1+4=3a2+2,即2a1+4=3a2 ②
解①②得,a1=1,a2=2.
∴an=
;
(Ⅱ)由(Ⅰ)知,
S2n=1+3+…+(2n-1)+2+2×3+…+2×3n-1
=
+2×
=n2+3n-1.
∵2S2n-na2n-1<λa2n恒成立,
∴2(n2+3n-1)-n(2n-1)<λ(2×3n-1),
即2×3n+n-2<λ(2×3n-1)恒成立.
∴λ>3+
恒成立.
令bn=
,则bn+1=
,
∴bn+1-bn=
-
=
.
∴当n≥3时,bn+1-bn<0,此时{bn}单调递减;
当n≤2时,bn+1-bn>0,此时{bn}单调递增.
∴b3最大,b3=
.
∴λ>
.
由a3+a5=a4+2,得a1+2+a1+4=3a2+2,即2a1+4=3a2 ②
解①②得,a1=1,a2=2.
∴an=
|
(Ⅱ)由(Ⅰ)知,
S2n=1+3+…+(2n-1)+2+2×3+…+2×3n-1
=
| n(1+2n-1) |
| 2 |
| 1-3n |
| 1-3 |
∵2S2n-na2n-1<λa2n恒成立,
∴2(n2+3n-1)-n(2n-1)<λ(2×3n-1),
即2×3n+n-2<λ(2×3n-1)恒成立.
∴λ>3+
| n-2 |
| 2×3n-1 |
令bn=
| n-2 |
| 2×3n-1 |
| n-1 |
| 2×3n |
∴bn+1-bn=
| n-1 |
| 2×3n |
| n-2 |
| 2×3n-1 |
| 5-2n |
| 2×3n |
∴当n≥3时,bn+1-bn<0,此时{bn}单调递减;
当n≤2时,bn+1-bn>0,此时{bn}单调递增.
∴b3最大,b3=
| 1 |
| 18 |
∴λ>
| 55 |
| 18 |
点评:本题考查等差数列和等比数列的通项公式,是数列与不等式的综合题,训练了分离变量法,考查了数列的函数特性,是中档题.

练习册系列答案
相关题目
 已知圆锥的侧面展开图是圆心角为120°的扇形,且圆锥的全面积为
已知圆锥的侧面展开图是圆心角为120°的扇形,且圆锥的全面积为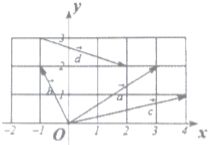 如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底.
如图所示,在平面直角坐标系xOy中,取x轴、y轴正方向上的单位向量为基底. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<