题目内容
9.设抛物线y2=-12x上一点P到y轴的距离是1,则点P到该抛物线焦点的距离是4.分析 求得抛物线的焦点坐标及准线方程,由抛物线的定义可知:P到焦点的距离等于P到准线的距离,则丨PF丨=4.
解答 解:由抛物线焦点F(-3,0),准线方程x=3,
由P到y轴的距离是1,则P到准线x=3的距离d=4,
则P到焦点的距离等于P到准线的距离,则丨PF丨=4,
故答案为:4.
点评 本题考查抛物线的定义,考查抛物线的焦点坐标及准线方程,考查计算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
19.函数f(x)=$\frac{1}{{\sqrt{x+1}}}$+$\sqrt{4-2x}$的定义域为( )
| A. | [一1,2] | B. | (一1,2] | C. | [2,+∞) | D. | [1,+∞) |
19.随着经济社会的发展,消费者对食品安全的关注度越来越高,通过随机询问某地区110名居民在购买食品时是否看生产日期与保质期等内容,得到如下的列联表:
年龄与看生产日期与保质期列联表 单位:名
(1)从这50名60岁以上居民中按是否看生产日期与保质期采取分层抽样,抽取一个容量为5的样本,问样本中看与不看生产日期与保质期的60岁以上居民各有多少名?
(2)从(1)中的5名居民样本中随机选取两名作深度访谈,求选到看与不看生产日期与保质期的60岁以上居民各1名的概率;
(3)根据以上列联表,问有多大把握认为“年龄与在购买食品时看生产日期与保质期”有关?
附:下面的临界值表供参考:
年龄与看生产日期与保质期列联表 单位:名
| 60岁以下 | 60岁以上 | 总计 | |
| 看生产日期与保质期 | 50 | 30 | 80 |
| 不看生产日期与保质期 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(2)从(1)中的5名居民样本中随机选取两名作深度访谈,求选到看与不看生产日期与保质期的60岁以上居民各1名的概率;
(3)根据以上列联表,问有多大把握认为“年龄与在购买食品时看生产日期与保质期”有关?
附:下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
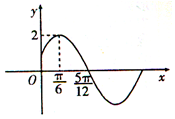 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.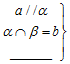 $\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β.
$\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β.