题目内容
14.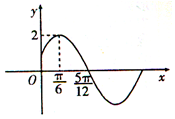 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$-\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式
(2)如何由函数y=2sinx的图象通过适当的变换得到函数f(x)的图象,写出变换过程.
分析 (1)由题意求出A,T,利用周期公式求出ω,利用当x=$\frac{π}{6}$时取得最大值2,求出φ,得到函数的解析式,即可;
(2)利用三角函数图象变换规律,即可得出结论.
解答 解:(1)由题意可知A=2,T=4($\frac{5}{12}π-\frac{π}{6}$)=π,ω=2,
当x=$\frac{π}{6}$时取得最大值2,所以 2=2sin(2x+φ),所以φ=$\frac{π}{6}$,
函数f(x)的解析式:f(x)=2sin(2x+$\frac{π}{6}$);
(2)函数y=2sinx的图象,先向左平移$\frac{π}{6}$个单位,得到f(x)=2sin(x+$\frac{π}{6}$),再横坐标变为原来的$\frac{1}{2}$,纵坐标不变,得到f(x)=2sin(2x+$\frac{π}{6}$).
点评 本题是基础题,考查由y=Asin(ωx+φ)的部分图象确定其解析式,注意函数的周期的求法,考查计算能力,常考题型.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
4.有矩形铁板,其长为6,宽为4,需从四个角上剪掉边长为 x 的四个小正方形,将剩余部分折成一个无盖的长方体盒子,要使容积最大,则 x 等于( )
| A. | $\frac{5-\sqrt{7}}{3}$ | B. | $\frac{5+\sqrt{7}}{3}$ | C. | $\frac{7-\sqrt{5}}{3}$ | D. | $\frac{7+\sqrt{5}}{3}$ |
5.已知$tanα=\frac{1}{2}$,则cos2α=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $±\frac{2}{5}$ | D. | $±\frac{3}{5}$ |
19.双曲线$\frac{y^2}{3}-\frac{x^2}{6}=1$的一个焦点坐标为( )
| A. | (3,0) | B. | (0,3) | C. | $(\sqrt{3},0)$ | D. | $(0,\sqrt{3})$ |
4.同时具有以下性质:“①最小正周期是π;②图象关于直线x=$\frac{π}{3}$对称;③在$[-\frac{π}{6},\frac{π}{3}]$上是增函数;④一个对称中心为$(\frac{π}{12},0)$”的一个函数是( )
| A. | $y=sin(\frac{x}{2}+\frac{π}{6})$ | B. | $y=sin(2x+\frac{π}{3})$ | C. | $y=sin(2x-\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{3})$ |