题目内容
20.函数f(x)=($\frac{1-{2}^{x}}{1+{2}^{x}}$)cosx的图象大致为( )| A. | 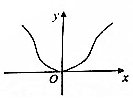 | B. | 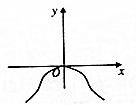 | C. | 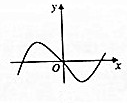 | D. | 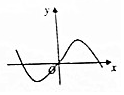 |
分析 利用函数的零点排除选项,然后通过特殊点的位置判断即可.
解答 解:函数f(x)=($\frac{1-{2}^{x}}{1+{2}^{x}}$)cosx,当x=$\frac{π}{2}$时,是函数的一个零点,属于排除A,B,当x∈(0,1)时,cosx>0,
$\frac{1-{2}^{x}}{1+{2}^{x}}$<0,函数f(x)=($\frac{1-{2}^{x}}{1+{2}^{x}}$)cosx<0,函数的图象在x轴下方.
排除D.
故选:C.
点评 本题考查函数的图象的判断与应用,考查函数的零点以及特殊值的计算,是中档题.

练习册系列答案
相关题目
11.“a2>1”是“a3>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.“a>b”是“ac2>bc2”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知$tanα=\frac{1}{2}$,则cos2α=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $±\frac{2}{5}$ | D. | $±\frac{3}{5}$ |