题目内容
1.已知命题: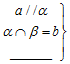 $\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β.
$\end{array}}\right\}$⇒a∥b,在“横线”处补上一个条件使其构成真命题(其中a、b为直线,α,β为平面),这个条件是a∥β.
分析 由题意设α∩β=b,a∥α,a∥β,然后过直线a作与α、β都相交的平面γ,利用平面与平面平行的性质进行求解
解答 解:∵α∩β=b,a∥α,设a∥β,
过直线a作与α、β都相交的平面γ,
记α∩γ=d,β∩γ=c,
则a∥d且a∥c,
∴d∥c.
又d?α,α∩β=l,
∴d∥l.∴a∥d.
∴$\left.\begin{array}{l}{a∥α}\\{α∩β=b}\\{a∥β}\end{array}\right\}$⇒a∥b
故答案为:a∥β.
点评 本题考查的知识点是直线与平面平行的性质定理的应用,熟练掌握直线与平面平行判断的方法及必要的条件是解答本题的关键.

练习册系列答案
相关题目
11.“a2>1”是“a3>1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.设集合A={x|1<x<2},B={x|x<a}满足A?B,则实数a的取值范围是( )
| A. | [2,+∞) | B. | (-∞,1] | C. | [1,+∞) | D. | (-∞,2] |
13.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F(c,0),作圆x2+y2=$\frac{{a}^{2}}{4}$的切线,切点为E,延长FE交双曲线左支于点M,且E是MF的中点,则双曲线离心率为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | 2$\sqrt{10}$ |