题目内容
以下命题:
①任意向量
2,有
2=|
|2成立;
②存在复数z,有z2=|z|2成立
③若ξ~B(4,0.25),则Dξ=1;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是真命题
其中正确命题的个数为( )
①任意向量
| a |
| a |
| a |
②存在复数z,有z2=|z|2成立
③若ξ~B(4,0.25),则Dξ=1;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是真命题
其中正确命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:运用平面向量的数量积的定义可判断①;考虑复数为实数时,等式成立,即可判断②;由二项分布的期望和方差公式即可判断③;由复合命题的真假性可判断④.
解答:
解:①由于
2=|
|•|
|•cos0=|
|2,故①正确;
②当复数z为实数时,有z2=|z|2成立,当复数z为虚数时,z2≠|z|2,故②正确;
③若ξ~B(4,0.25),则Dξ=4×0.25×(1-0.25)=0.75,故③不正确;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是假命题,故④不正确.
故正确个数为2.
故选B.
| a |
| a |
| a |
| a |
②当复数z为实数时,有z2=|z|2成立,当复数z为虚数时,z2≠|z|2,故②正确;
③若ξ~B(4,0.25),则Dξ=4×0.25×(1-0.25)=0.75,故③不正确;
④如果命题p是真命题,命题q是假命题,则命题“p且q”是假命题,故④不正确.
故正确个数为2.
故选B.
点评:本题以命题的真假为载体,考查平面向量的数量积的定义,复数的概念,以及二项分布的期望和方差,考查复合命题的真假,是一道基础题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
若x>1,则函数y=
+x的最小值是( )
| 1 |
| x-1 |
| A、3 | B、4 | C、2 | D、8 |
执行所示的程序框图,若输出的S是2047,则判断框内应填写( )


| A、n≤9? | B、n≤10? |
| C、n≥10? | D、n≥11? |

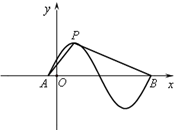 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若cos∠APB=-