题目内容
已知集合A={y|y=sinx，x∈R}，B={x|x=2n+1，n∈Z}，则A∩B= ．
考点：交集及其运算
专题：集合
分析：根据正弦函数的值域确定出y的范围，得到集合A，集合B表示奇数集，求出两集合的交集即可．
解答：
解：由A中的y=sinx，得到-1≤sinx≤1，即-1≤y≤1，
∴A=[-1，1]，
集合B中x=2n+1，n∈Z，表示所有的奇数，
∴B={…，-2，-1，0，1，2，…}
则A∩B={-1，1}．
故答案为：{-1，1}
∴A=[-1，1]，
集合B中x=2n+1，n∈Z，表示所有的奇数，
∴B={…，-2，-1，0，1，2，…}
则A∩B={-1，1}．
故答案为：{-1，1}
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
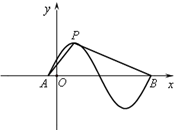函数y=sin（ωx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，若cos∠APB=-