题目内容
已知数列{an},{bn}满足:a1=
,a2=1,an+1=an-
an-1(n≥2);an=
(n∈N*).
(Ⅰ)计算b1,b2,b3,并求数列{bn},{an}的通项公式;
(Ⅱ)证明:对于任意的n>3,都有a1+a2+a3>a4+a5+…+an.
| 1 |
| 2 |
| 1 |
| 4 |
| bn |
| 2n |
(Ⅰ)计算b1,b2,b3,并求数列{bn},{an}的通项公式;
(Ⅱ)证明:对于任意的n>3,都有a1+a2+a3>a4+a5+…+an.
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)直接由数列递推式求得a3,然后把数列{an}的前3项分别代入an=
求得b1,b2,b3.将an=
•bn,an+1=
•bn+1,an-1=
•bn-1代入an+1=an-
an-1化简得:bn-1+bn+1=2bn,说明数列{bn}是等差数列,求其通项公式后代入an=
得数列{an}的通项公式;
(Ⅱ)利用错位相减法求出数列{an}的前n项和,得到对于任意的n∈N*,总有Sn<4,再求出a1+a2+a3=
>2得答案.
| bn |
| 2n |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n-1 |
| 1 |
| 4 |
| bn |
| 2n |
(Ⅱ)利用错位相减法求出数列{an}的前n项和,得到对于任意的n∈N*,总有Sn<4,再求出a1+a2+a3=
| 19 |
| 8 |
解答:
(Ⅰ)解:由a1=
,a2=1,an+1=an-
an-1(n≥2),得a3=a2-
a1=1-
×
=
,
又an=
,
∴b1=2a1=2×
=1,b2=4a2=4,b3=8a3=8×
=7;
将an=
•bn,an+1=
•bn+1,an-1=
•bn-1代入an+1=an-
an-1化简得:bn-1+bn+1=2bn,
由等差中项的概念知数列{bn}是等差数列.
由b1=1,b2=4知其公差为3,故bn=3n-2.
代入an=
,得an=
;
(Ⅱ)证明:设数列{an}的前n项和为Sn.
则Sn=
+
+
+…+
,
Sn=
+
+…+
+
,
两式相减可得:
∴Sn=4-
.
可见,对于任意的n∈N*,总有Sn<4.
但a1+a2+a3=
>2,
故当n>3时,a4+a5+…+an<2<a1+a2+a3.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 8 |
又an=
| bn |
| 2n |
∴b1=2a1=2×
| 1 |
| 2 |
| 7 |
| 8 |
将an=
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n-1 |
| 1 |
| 4 |
由等差中项的概念知数列{bn}是等差数列.
由b1=1,b2=4知其公差为3,故bn=3n-2.
代入an=
| bn |
| 2n |
| 3n-2 |
| 2n |
(Ⅱ)证明:设数列{an}的前n项和为Sn.
则Sn=
| 1 |
| 2 |
| 4 |
| 22 |
| 7 |
| 23 |
| 3n-2 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 4 |
| 23 |
| 3n-5 |
| 2n |
| 3n-2 |
| 2n+1 |
两式相减可得:
|
∴Sn=4-
| 3n+4 |
| 2n |
可见,对于任意的n∈N*,总有Sn<4.
但a1+a2+a3=
| 19 |
| 8 |
故当n>3时,a4+a5+…+an<2<a1+a2+a3.
点评:本题是数列与不等式的综合题,考查了利用等差中项的概念确定数列为等差数列,考查了错位相减法求数列的和,考查了放缩法证明数列不等式,是压轴题.

练习册系列答案
相关题目
设-5<a<5,集合M={x∈N|2x-(a+5)x-10=0}.若M≠?,则满足条件的所有实数a的和等于( )
A、-
| ||
B、-
| ||
C、
| ||
| D、4 |
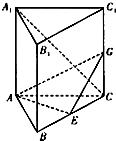 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.