题目内容
定义:如果一个数列从第二项起,每一项与前一项的差依次构成一个等比数列,则称这个数列为差等比数列,如果数列{an}满足an+1=3an-2an-1(n≥2),a1=1,a2=3.
(Ⅰ)求证:数列{an}是差等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)Sn是数列{an}的前n项和,如果对任意的正整数n(n≥4),不等式Sn≤kan-9k恒成立,求实数k的取值范围.
(Ⅰ)求证:数列{an}是差等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)Sn是数列{an}的前n项和,如果对任意的正整数n(n≥4),不等式Sn≤kan-9k恒成立,求实数k的取值范围.
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)把数列的递推式变形,得到an+1-an=2an-2an-1(n≥2),结合a2-a1=2≠0,可得数列{an}是差等比数列;
(Ⅱ)由数列{an+1-an}是等比数列求出数列{an}的通项公式;
(Ⅲ)求出数列{an}的前n项和,代入Sn≤kan-9k后分类k,构造函数g(n)=2+
,求出其最大值后得答案.
(Ⅱ)由数列{an+1-an}是等比数列求出数列{an}的通项公式;
(Ⅲ)求出数列{an}的前n项和,代入Sn≤kan-9k后分类k,构造函数g(n)=2+
| 18-n |
| 2n-10 |
解答:
(Ⅰ)证明:由an+1=3an-2an-1,得an+1-an=2an-2an-1(n≥2),
∵a2-a1=2≠0,
∴
=2,
∴数列{an}是差等比数列;
(Ⅱ)解:∵数列{an+1-an}是等比数列,首项a2-a1=2,公比为2,
∴an+1-an=2×2n-1=2n.
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+2+22+…+2n-1=2n-1.
∴an=2n-1;
(Ⅲ)解:Sn=(21-1)+(22-1)+…+(2n-1)
=(1+22+…+2n)-n=
-n
=2n+1-2-n.
由Sn≤kan-9k,得2n+1-2-n≤k(2n-10),
∵n≥4,
∴2n-10>0,
则k≥
=2+
.
令g(n)=2+
,
知n≥4时,g(n)max=g(4)=
,
∴k≥
.
∵a2-a1=2≠0,
∴
| an+1-an |
| an-an-1 |
∴数列{an}是差等比数列;
(Ⅱ)解:∵数列{an+1-an}是等比数列,首项a2-a1=2,公比为2,
∴an+1-an=2×2n-1=2n.
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=1+2+22+…+2n-1=2n-1.
∴an=2n-1;
(Ⅲ)解:Sn=(21-1)+(22-1)+…+(2n-1)
=(1+22+…+2n)-n=
| 1-2n+1 |
| 1-2 |
=2n+1-2-n.
由Sn≤kan-9k,得2n+1-2-n≤k(2n-10),
∵n≥4,
∴2n-10>0,
则k≥
| 2n+1-2-n |
| 2n-10 |
| 18-n |
| 2n-10 |
令g(n)=2+
| 18-n |
| 2n-10 |
知n≥4时,g(n)max=g(4)=
| 13 |
| 3 |
∴k≥
| 13 |
| 3 |
点评:本题考查了数列与不等式的综合,考查了等比关系的确定,训练了数列的分组求和,考查了分离变量法,训练了函数构造法,是压轴题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知四面体的各条棱长均为2,则它的表面积是( )
A、
| ||
B、2
| ||
C、4
| ||
D、8
|
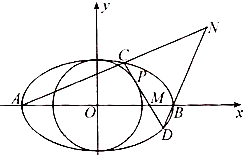 已知椭圆C1:
已知椭圆C1: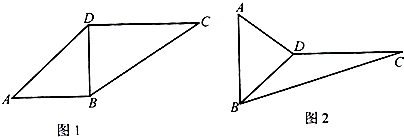
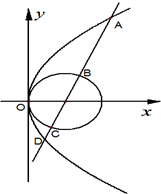 如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l
如图,抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点的直线l