题目内容
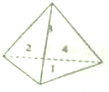 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.(1)求点P恰好返回A点的概率;
(2)在点P转一周恰能返回A点的所有结果中,求至少需投掷3次点P才能返回A的概率.
考点:n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:(1)由题意根据相互独立事件的概率乘法公式,分类讨论求得转一周之前点P恰好返回A点的概率.
(2)由(1),把投掷三次,点P恰好返回A点的概率和投掷四次,点P恰好返回A点的点P恰好返回A点的概率相加,即得所求.
(2)由(1),把投掷三次,点P恰好返回A点的概率和投掷四次,点P恰好返回A点的点P恰好返回A点的概率相加,即得所求.
解答:
解:(1)投掷一个质地均匀的正四面体,四面体每个面上的数字在底面上的概率是相等的,都等于
,
若投掷一次,点P恰好返回A点,则四面体的底面上的数字为4的概率为
,
若投掷二次,点P恰好返回A点,则四面体的底面上的数字分别为(1,3)、(3,1)、(2,2),
共3种结果,其概率为3×(
)3=
,
若投掷三次,点P恰好返回A点,则四面体的底面上的数字分别为(1,1,2)、(1,2,1)、(2,1,1),
共3种结果,其概率为 3×(
)3=
,
若投掷四次,点P恰好返回A点,则四面体的底面上的数字分别为(1,1,1,1),共一种结果,
其概率为(
)4=
.
综上可得,点P恰好返回A点的概率为
+
+
+
=
.
(2)由(1)可得,投掷三次,点P恰好返回A点的概率为 3×(
)3=
,
投掷四次,点P恰好返回A点的点P恰好返回A点的概率为
,
故至少需投掷3次点P才能返回A的概率为
+
=
.
在点P转一周恰能返回A点的所有的8个结果中,至少需投掷3次点P才能返回A的结果有:
(1,1,2)、(1,2,1)、(2,1,1)、(1,1,1,1),共4种结果,
故至少需投掷3次点P才能返回A的概率为
=
.
| 1 |
| 4 |
若投掷一次,点P恰好返回A点,则四面体的底面上的数字为4的概率为
| 1 |
| 4 |
若投掷二次,点P恰好返回A点,则四面体的底面上的数字分别为(1,3)、(3,1)、(2,2),
共3种结果,其概率为3×(
| 1 |
| 4 |
| 3 |
| 16 |
若投掷三次,点P恰好返回A点,则四面体的底面上的数字分别为(1,1,2)、(1,2,1)、(2,1,1),
共3种结果,其概率为 3×(
| 1 |
| 4 |
| 3 |
| 64 |
若投掷四次,点P恰好返回A点,则四面体的底面上的数字分别为(1,1,1,1),共一种结果,
其概率为(
| 1 |
| 4 |
| 1 |
| 256 |
综上可得,点P恰好返回A点的概率为
| 1 |
| 4 |
| 3 |
| 16 |
| 3 |
| 64 |
| 1 |
| 256 |
| 125 |
| 256 |
(2)由(1)可得,投掷三次,点P恰好返回A点的概率为 3×(
| 1 |
| 4 |
| 3 |
| 64 |
投掷四次,点P恰好返回A点的点P恰好返回A点的概率为
| 1 |
| 256 |
故至少需投掷3次点P才能返回A的概率为
| 3 |
| 64 |
| 1 |
| 256 |
| 13 |
| 256 |
在点P转一周恰能返回A点的所有的8个结果中,至少需投掷3次点P才能返回A的结果有:
(1,1,2)、(1,2,1)、(2,1,1)、(1,1,1,1),共4种结果,
故至少需投掷3次点P才能返回A的概率为
| 4 |
| 8 |
| 1 |
| 2 |
点评:本题主要考查相互独立事件的概率乘法公式,古典概型及其概率计算公式的应用,列举法,是解决古典概型问题的一种重要的解题方法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
满足A∪{-1,1}={-1,0,1}的集合A共有( )
| A、10个 | B、8个 | C、6个 | D、4个 |
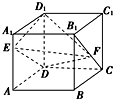 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
圆x2+(y-2)2=1的圆心到直线x+y-1=0的距离为( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、2
|
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|