题目内容
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由于双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,可得圆心(2,0)到渐近线的距离d=r,利用点到直线的距离公式即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:取双曲线的渐近线y=
x,即bx-ay=0.
∵双曲线
-
=1(a>0,b>0)的渐近线与(x-2)2+y2=1相切,
∴圆心(2,0)到渐近线的距离d=r,
∴
=1,化为2b=c,
两边平方得c2=4b2=4(c2-a2),化为3c2=4a2.
∴e=
=
故选:B.
| b |
| a |
∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
∴圆心(2,0)到渐近线的距离d=r,
∴
| 2b | ||
|
两边平方得c2=4b2=4(c2-a2),化为3c2=4a2.
∴e=
| c |
| a |
2
| ||
| 3 |
故选:B.
点评:本题考查了双曲线的渐近线及其离心率、点到直线的距离公式、直线与圆相切的性质等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
考虑一元二次方程x2+mx+n=0,其中m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.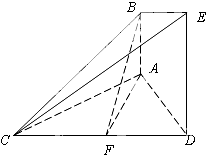 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.