题目内容
设集合M={x|y=
},N={y|y=3-2x},则M∩N= .
| 3-2x |
考点:交集及其运算
专题:函数的性质及应用,集合
分析:由3-2x≥0求出函数y=
的定义域M,由2x≥0求出函数y=3-2x的值域N,再由交集的运算求出M∩N.
| 3-2x |
解答:
解:由3-2x≥0得,x≤
,则函数y=
的定义域M=(-∞,
],
由2x≥0得,3-2x≤3,则函数y=3-2x的值域N=(-∞,3),
所以M∩N=(-∞,
],
故答案为:(-∞,
].
| 3 |
| 2 |
| 3-2x |
| 3 |
| 2 |
由2x≥0得,3-2x≤3,则函数y=3-2x的值域N=(-∞,3),
所以M∩N=(-∞,
| 3 |
| 2 |
故答案为:(-∞,
| 3 |
| 2 |
点评:本题考查交集及其运算,以及函数的定义域、值域的求法,属于基础题.

练习册系列答案
相关题目
若集合A={x|x2-1≤0},B={x|
≤0},则A∩B=( )
| x-2 |
| x |
| A、{x|-1≤x<0} |
| B、{x|0<x≤1} |
| C、{x|0≤x≤2} |
| D、{x|0≤x≤1} |
等差数列{an}的前3项和为30,前6项和为100,则它的前9项和是( )
| A、130 | B、170 |
| C、210 | D、260 |
若函数f(x)=
,则f(log42)=( )
|
| A、1 | B、2 | C、3 | D、4 |
设a=lg3,b=(lg3)2,c=lg
,则有( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、b>c>a |
| D、b>a>c |
已知集合A={0,1},B={x|x2∈A},则( )
| A、A⊆B | B、B⊆A |
| C、A=B | D、A∈B |
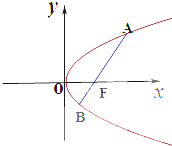 如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点
如图,给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点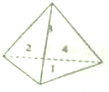 把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进,现在投掷一个质地均匀的正四面体,它的四个面上分别写有1,2,3,4四个数字,P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.