题目内容
2.已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8.(Ⅰ) 求动圆圆心的轨迹C的方程;
(Ⅱ) 已知点B(-3,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
分析 (Ⅰ) 根据勾股定理,建立方程,进而求得动圆圆心的轨迹C的方程;
(Ⅱ)设P(x1,y1),Q(x2,y2),由题意,直线PQ的方程代入化简,利用角平分线的性质可得kPB=-kQB,可化为:-16tm+(3+m)8t=0,所以:m=3,l:x=ty+3,即可得到定点.
解答 解:(Ⅰ)设动圆圆心P(x,y),则|PM|2=|PA|2=42+x2即:(x-4)2+y2=42+x2,
即动圆圆心的轨迹方程为:y2=8x,
(Ⅱ) 设两点P(x1,y1),Q(x2,y2)设不垂直于x轴的直线:l:x=ty+m(t≠0),则$\left\{{\begin{array}{l}{x=ty+m}\\{{y^2}=8x}\end{array}}\right.$有:y2-8ty-8m=0,所以:y1+y2=8t,y1y2=-8m,
因为x轴是∠PBQ的角平分线,
所以:kBP+kBQ=0即:$\frac{y_1}{{{x_1}+3}}+\frac{y_2}{{{x_2}+3}}=0$即:2ty1y2+(m+3)(y1+y2)=0,
则:-16tm+(3+m)8t=0,所以:m=3l:x=ty+3所以直线l过定点(3,0).
点评 本题综合考查了抛物线的标准方程、直线与抛物线相交问题、直线方程及过定点问题、斜率计算公式等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.扇形的半径为1,周长为4,则扇形的圆心角弧度数的绝对值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知幂函数f(x)的图象过点$(2,\frac{{\sqrt{2}}}{2})$,则f(x)是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
7.已知A={x|x+1>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
14.若实数k满足0<k<9,则曲线$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9-k}$=1与曲线$\frac{{x}^{2}}{25-k}$-$\frac{{y}^{2}}{9}$=1的( )
| A. | 离心率相等 | B. | 虚半轴长相等 | C. | 实半轴长相等 | D. | 焦距相等 |
12.设p:实数x,y满足(x-2)2+(y-2)2≤8,q:实数x,y满足$\left\{\begin{array}{l}y≥x-2\\ y≥2-x\\ y≤2\end{array}\right.$,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
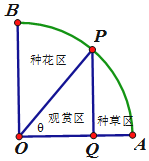 如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP
如图,一个圆心角为直角的扇形AOB 花草房,半径为1,点P 是花草房弧上一个动点,不含端点,现打算在扇形BOP 内种花,PQ⊥OA,垂足为Q,PQ 将扇形AOP