扇形的半径为1.周长为4.则扇形的圆心角弧度数的绝对值为( )A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

12．扇形的半径为1，周长为4，则扇形的圆心角弧度数的绝对值为（　　）

A．

B．

C．

D．

分析利用扇形的周长及半径，可求弧长，利用弧长公式即可求得扇形的圆心角的弧度数，从而得解．

解答解：设扇形的圆心角的弧度数为α，扇形弧长为l，周长为L，圆的半径为r，
由题意可得：r=1，L=4，
可得：l=L-2r=4-2×1=2，
则由l=αr，可得：α=$\frac{2}{1}$=2．
故选：B．

点评本题考查扇形的周长与弧长公式，考查了数形结合思想，属于基础题．

练习册系列答案

相关题目

15．抛物线y=-$\frac{1}{8}{x}^{2}$的准线方程是（　　）

3．已知函数f（x）=2sin（2ωx+$\frac{π}{3}$）（ω＞0），最小正周期为π
（1）求ω的值；
（2）将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度，再将所得图象各点的横坐标缩小为原来的$\frac{1}{2}$（纵坐标不变），得到函数g（x）的图象，求g（x）的单调区间．

20．设x，y∈R，下列不等式成立的是（　　）

7．集合M={x|0＜x≤3}，N={x|0＜x≤2}，则a∈M是a∈N的（　　）

	A．	充分不必要条件		B．	必要不充分条件
	C．	充要条件		D．	既不充分也不必要条件

17．已知函数f（x）=sin2x+sin（2x-$\frac{π}{3}$）．
（1）求f（x）的最小正周期；
（2）将f（x）的图象沿x轴向左平移m（m＞0）个单位，所得函数g（x）的图象关于直线x=$\frac{π}{8}$对称，求m的最小值及m最小时g（x）在$[0，\frac{π}{4}]$上的值域．

4．

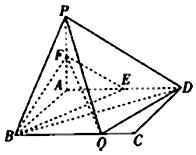如图，在矩形ABCD中，AB=1，AD=a，PA⊥平面ABCD，且PA=1，E，F分别为AD，PA中点，在BC上有且只有一个点Q，使得PQ⊥QD．
（1）求证：平面BEF∥平面PDQ；
（2）求二面角E-BF-Q的余弦值．

1．

如图，在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=2，CD=4．
（1）求证：BE∥平面PAD；
（2）求证：平面PBC⊥平面PBD；
（3）设Q为棱PC上一点，$\overrightarrow{CQ}$=λ$\overrightarrow{CP}$，试确定λ的值使得二面角Q-BD-P为60°．

2．已知动圆过定点A（4，0），且在y轴上截得的弦MN的长为8．
（Ⅰ）求动圆圆心的轨迹C的方程；
（Ⅱ）已知点B（-3，0），设不垂直于x轴的直线l与轨迹C交于不同的两点P，Q，若x轴是∠PBQ的角平分线，证明直线l过定点．

试题分类