题目内容

7．已知A={x|x+1＞0}，B={-2，-1，0，1}，则（∁RA）∩B=（　　）
A．A={0，1，2}B．{-2}C．{-1，0，1}D．{-2，-1}

分析 化简集合A、求出∁RA，再计算（∁RA）∩B即可．

解答 解：A={x|x+1＞0}={x|x＞-1}，B={-2，-1，0，1}，
则∁RA={x|x≤-1}，
（∁RA）∩B={-2，-1}．
故选：D．

点评 本题考查了集合的化简与运算问题，是基础题目．

练习册系列答案
相关题目
17．已知函数f（x）=sin2x+sin（2x-$\frac{π}{3}$）．
（1）求f（x）的最小正周期；
（2）将f（x）的图象沿x轴向左平移m（m＞0）个单位，所得函数g（x）的图象关于直线x=$\frac{π}{8}$对称，求m的最小值及m最小时g（x）在$[0，\frac{π}{4}]$上的值域．
18．在空间中，已知$\overrightarrow{AB}$=（2，4，0），$\overrightarrow{DC}$=（-1，3，0），则异面直线AB与DC所成角θ的大小为（　　）
A．45°B．90°C．120°D．135°
15．已知点A的坐标为（4，2），F是抛物线y2=2x的焦点，点M是抛物线上的动点，当|MF|+|MA|取得最小值时，点M的坐标为（2，2）．
2．已知动圆过定点A（4，0），且在y轴上截得的弦MN的长为8．
（Ⅰ） 求动圆圆心的轨迹C的方程；
（Ⅱ） 已知点B（-3，0），设不垂直于x轴的直线l与轨迹C交于不同的两点P，Q，若x轴是∠PBQ的角平分线，证明直线l过定点．
12．已知f（x）=-cos2x+$\sqrt{3}$sinxcosx
（Ⅰ）求函数f（x）的最小值并求函数取得最小值时自变量x的值；
（Ⅱ）求函数f（x）的单调增区间．
19．已知集合A={x|（3-x）（x+1）＞0}，B={x|-2＜x≤1}，则A∩B=（　　）
A．（-1，1]B．（-2，3]C．（-2，-1）D．（-2，1-）∪[1，3）
16．已知幂函数$f（x）={（m-1）^2}{x^{{m^2}-4m+2}}$在（0，+∞）上单调递增，函数g（x）=2x-t，?x1∈[1，6）时，总存在x2∈[1，6）使得f（x1）=g（x2），则t的取值范围是（　　）
A．∅B．t≥28或t≤1C．t＞28或t＜1D．1≤t≤28
17．如图，在三棱柱ABC-A1B1C1中，M为A1C1的中点，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{A{A_1}}$=$\overrightarrow{c}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，则$\overrightarrow{BM}$可表示为（　　）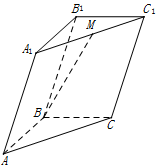
A．-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$B．$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$C．-$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$D．$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网