题目内容
13.已知幂函数f(x)的图象过点$(2,\frac{{\sqrt{2}}}{2})$,则f(x)是( )| A. | 偶函数 | B. | 奇函数 | ||
| C. | 定义域上的增函数 | D. | 定义域上的减函数 |
分析 设f(x)=xα,把点(2,$\frac{\sqrt{2}}{2}$)代入解出即可.
解答 解:设f(x)=xα,
∵幂函数y=f(x)图象过点(2,$\frac{\sqrt{2}}{2}$),
∴$\frac{\sqrt{2}}{2}$${2}^{-\frac{1}{2}}$=2α,
解得α=-$\frac{1}{2}$,
∴f(x)=${x}^{-\frac{1}{2}}$,
是定义域上的减函数,
故选:D.
点评 本题考查了幂函数的定义及其性质,属于基础题.

练习册系列答案
相关题目
18.在空间中,已知$\overrightarrow{AB}$=(2,4,0),$\overrightarrow{DC}$=(-1,3,0),则异面直线AB与DC所成角θ的大小为( )
| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
5.下列向量组中,能作为平面内所有向量的基底的是( )
| A. | $\overrightarrow{a}$=(0,0),$\overrightarrow{b}$=(1,-2) | B. | $\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(5,7) | C. | $\overrightarrow{a}$=(3,5),$\overrightarrow{b}$=(6,10) | D. | $\overrightarrow{a}$=(2,-3),$\overrightarrow{b}$=(4,-6) |
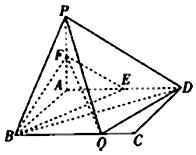 如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD.
如图,在矩形ABCD中,AB=1,AD=a,PA⊥平面ABCD,且PA=1,E,F分别为AD,PA中点,在BC上有且只有一个点Q,使得PQ⊥QD. 如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
如图,在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.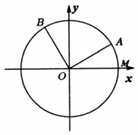 如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.
如图,已知单位圆O与x轴正半轴相交于点M,点A,B在单位圆上,其中点A在第一象限,且∠AOB=$\frac{π}{2}$,记∠MOA=α,∠MOB=β.